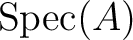Next: Benefit of being a Up: sheaves Previous: presheaves
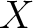 be a topological space. A presheaf
be a topological space. A presheaf
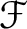 of rings
over
of rings
over 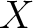 is called a sheaf if
for any open set
is called a sheaf if
for any open set
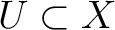 and for any
open covering
and for any
open covering
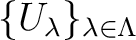 of
of 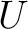 ,
it satisfies the following
conditions.
,
it satisfies the following
conditions.
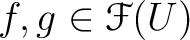 such that
such that
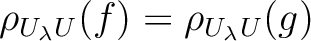
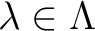 , then we have
, then we have 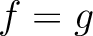
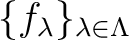 such that
such that
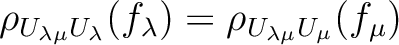
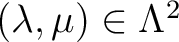 , then we have
a section
, then we have
a section
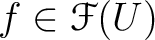 such that
such that
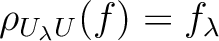
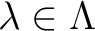 .
.
We may similarly define sheaf of sets, sheaf of modules, etc.
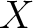 be a topological set with an open base
be a topological set with an open base
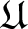 .
To define a sheaf
.
To define a sheaf
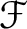 over
over 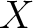 we only need to
define
we only need to
define
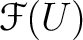 for every member
for every member 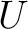 of
of
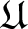 and
check the sheaf axiom for open bases.
In precise, given such data, we may always find a unique sheaf
and
check the sheaf axiom for open bases.
In precise, given such data, we may always find a unique sheaf
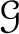 on
on 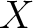 such that
such that
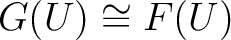 holds in a natural way.
(That means, the isomorphism commutes
with restrictions wherever they are defined.)
holds in a natural way.
(That means, the isomorphism commutes
with restrictions wherever they are defined.)
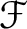 be such. For any open set
be such. For any open set
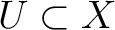 , we define
a presheaf
, we define
a presheaf
 by the following formula.
by the following formula.
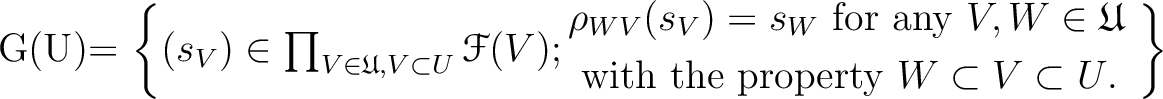
 is defined in an obvious manner.
is defined in an obvious manner.
Then it is easy to see that
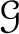 satisfies the sheaf axiom and that
satisfies the sheaf axiom and that
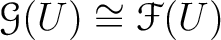
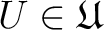 in a natural way.
in a natural way.
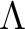
 be a ring.
be a ring.
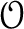 of rings on
of rings on
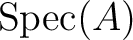 which
is defined uniquely by the property
which
is defined uniquely by the property
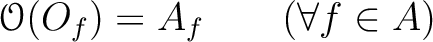
 -module
-module  we have a sheaf
we have a sheaf
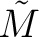 of modules on
of modules on
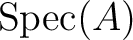 which
is defined uniquely by the property
which
is defined uniquely by the property
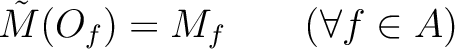
 -module
-module 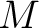 , the sheaf
, the sheaf
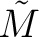 is a sheaf of
is a sheaf of
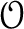 -modules on
-modules on
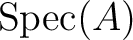 . That means, it is a sheaf of modules
over
. That means, it is a sheaf of modules
over
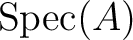 with an additional
with an additional
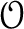 -action (which is
defined in an obvious way.)
-action (which is
defined in an obvious way.)
From the previous Lemma, we only need to prove locality and gluing lemma for
open sets of the form 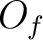 . That means, in proving the properties
(1) and (2) of Definition 7.19, we may assume that
. That means, in proving the properties
(1) and (2) of Definition 7.19, we may assume that
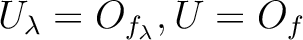 for some elements
for some elements
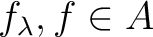 .
.
Furthermore, in doing so we may use the identification
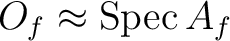 .
By replacing
.
By replacing  by
by 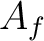 , this means that we may assume that
, this means that we may assume that
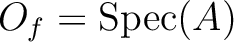 .
.
To sum up, we may assume
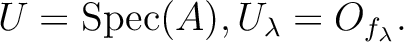
To simplify the notation, in the rest of the proof, we shall denote by
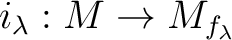
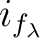 .
Furthermore, for any pair
.
Furthermore, for any pair
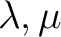 of the index set,
we shall denote by
of the index set,
we shall denote by
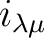 the canonical map
the canonical map
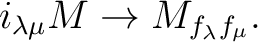
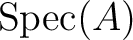 (Theorem 7.12) implies that
there exist finitely many open sets
(Theorem 7.12) implies that
there exist finitely many open sets
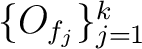 among
among 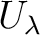 such that
such that
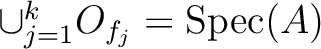 .
In particular there exit elements
.
In particular there exit elements
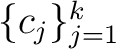 of
of  such that
such that
| (PU) | 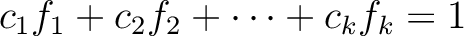 |
Let 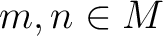 be elements such that
be elements such that
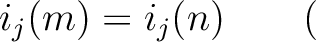 in
in 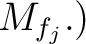
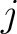 , there exist positive integers
, there exist positive integers 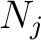 such that
such that
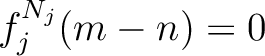
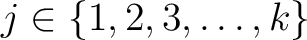 .
Let us take the maximum
.
Let us take the maximum 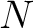 of
of 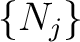 . It is easy to see that
. It is easy to see that
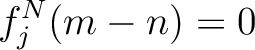
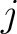 . On the other hand, taking
. On the other hand, taking 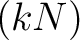 -th power of the equation
(PU) above, we may find elements
-th power of the equation
(PU) above, we may find elements
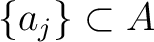 such that
such that
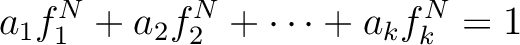
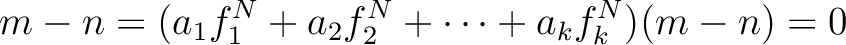
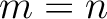 .
.
Gluing lemma:
Let
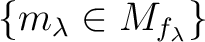 be given
such that they satisfy
be given
such that they satisfy
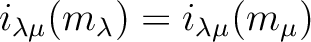
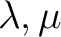 .
We fist choose a finite subcovering
.
We fist choose a finite subcovering
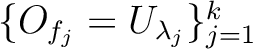 of
of
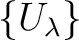 .
Then we may choose a positive integer
.
Then we may choose a positive integer 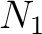 such that
such that
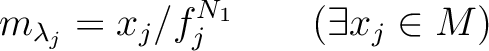
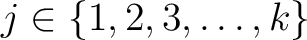 .
.
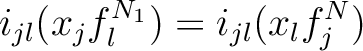
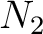 such that
such that
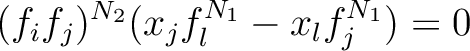
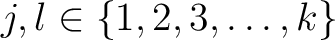 .
We rewrite the above equation as follows.
.
We rewrite the above equation as follows.
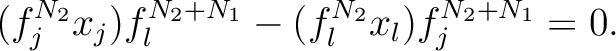
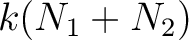 -th power of the equation (PU),
we may see that there exist elements
-th power of the equation (PU),
we may see that there exist elements
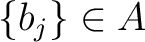 such that
such that
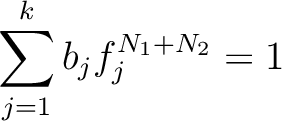
Now we put
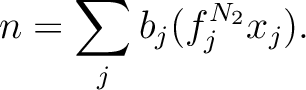
Then since for any 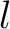
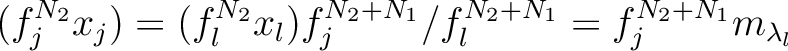
 , we have
, we have
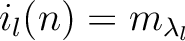 .
.
Now, take any other open set
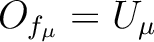 from the covering
from the covering
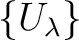 .
.
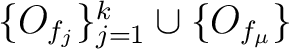 is again a finite open
covering of
is again a finite open
covering of
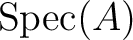 .
We thus know from the argument above that there exists an element
.
We thus know from the argument above that there exists an element 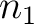 of
of
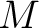 such that
such that

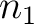 coincides with
coincides with 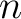 .
In particular,
.
In particular,
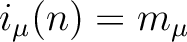 holds.
This means
holds.
This means 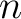 satisfies the requirement for the “glued object”.
satisfies the requirement for the “glued object”.
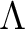
 be a commutative ring. Let
be a commutative ring. Let 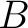 be a non-commutative ring which
contains
be a non-commutative ring which
contains  as a central subalgebra (that means,
as a central subalgebra (that means,
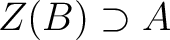 ).
Then there exists a sheaf
).
Then there exists a sheaf 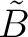 of
of
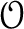 -algebras over
-algebras over