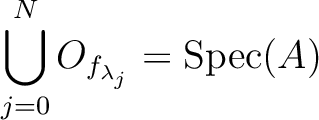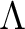Next: closed subsets Up: Zariski topology on affine Previous: Zariski topology on affine
 , the spectrum
, the spectrum
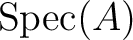 of
of  (equipped with
the Zariski topology) is a compact set.
(equipped with
the Zariski topology) is a compact set.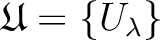 be an open covering of
be an open covering of
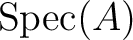 .
We want to find a finite subcovering of
.
We want to find a finite subcovering of
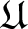 .
.
For any
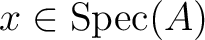 , we have a index
, we have a index 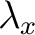 and an
open subset
and an
open subset 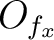 of
of
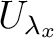 such that
such that
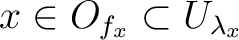
 by
by
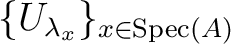 if necessary,
we may assume each
if necessary,
we may assume each 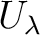 is of the form
is of the form
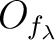 for some
for some
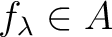 .
.
Now,
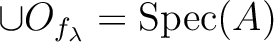
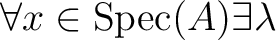 such that
such that 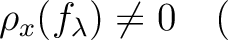 that means,
that means, 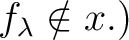
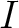 defined by
defined by
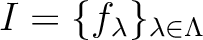
 . Assume the contrary. Using Zorn's lemma we may always
obtain an maximal ideal
. Assume the contrary. Using Zorn's lemma we may always
obtain an maximal ideal
 of
of  which contains
which contains 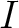 .
This is a contradiction to the fact mentioned above.
.
This is a contradiction to the fact mentioned above.
Thus we have proved that 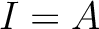 . In particular, we may find a relation
. In particular, we may find a relation
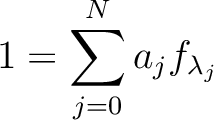
 , index sets
, index sets
 ,
and elements
,
and elements 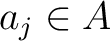 . This clearly means that
. This clearly means that