Next: sheaves Up: sheaves Previous: A convention.
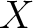 be a topological space. We say “a presheaf
be a topological space. We say “a presheaf
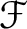 of rings over
of rings over 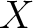 is
given” if we are given the following data.
is
given” if we are given the following data.
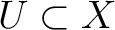 , a ring denoted by
, a ring denoted by
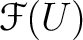 .
(which is called the ring of sections of
.
(which is called the ring of sections of
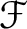 on
on 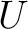 .)
.)
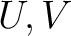 of open subsets of
of open subsets of 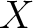 such that
such that
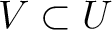 , a ring homomorphism (called restriction)
, a ring homomorphism (called restriction)
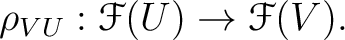
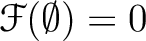 .
.
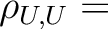 identity for any open subset
identity for any open subset
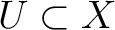 .
.
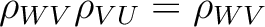
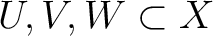 such that
such that
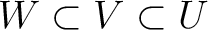 .
.