Next: A convention. Up: , , and the Previous: closed subsets
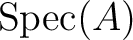 of a ring
of a ring  carries one more important structure.
Namely, its structure sheaf.
carries one more important structure.
Namely, its structure sheaf.
We will firstly review some definitions and first properties of sheaves.
To illustrate the idea, we recall an easy lemma in topology.
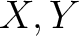 be a topological spaces.
Let
be a topological spaces.
Let
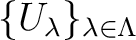 be an open covering of
be an open covering of 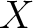 .
.
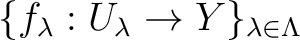 such that
such that
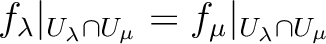
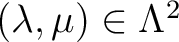 , then
we have a unique continuous map
, then
we have a unique continuous map 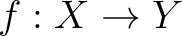 such that
such that
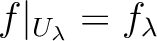
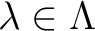 .
.
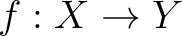 ,
then we obtain a collection of maps
,
then we obtain a collection of maps
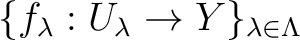 by restriction.
by restriction.
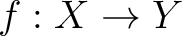
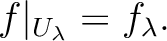
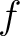 is proved by verifying that the
inverse image of any open set
is proved by verifying that the
inverse image of any open set
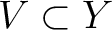 by
by 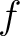 is open in
is open in 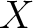 .
.