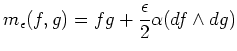
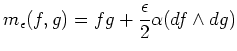
2-フォームの空間の双対の元 ![]() (ポアソン括弧
(ポアソン括弧
![]() )
を与える事により決まるこのような量子化は
)
を与える事により決まるこのような量子化は ![]() 多様体の
を相手にしている場合にはポアソン多様体の量子化として良く知られたものである。
(なお、この一次の変形が高次の変形に延びるための、いわゆる
可積分条件は、ポアソン括弧
多様体の
を相手にしている場合にはポアソン多様体の量子化として良く知られたものである。
(なお、この一次の変形が高次の変形に延びるための、いわゆる
可積分条件は、ポアソン括弧
![]() が
Jacobi の恒等式を満たす事であることが知られている。
(この周辺のことについては例えば[9]を参照のこと))
が
Jacobi の恒等式を満たす事であることが知られている。
(この周辺のことについては例えば[9]を参照のこと))
(余談であるが
リーマン多様体の無限小変形では、![]() と
と
![]() のセクションが肩を
並べて出て来ることになるので、
のセクションが肩を
並べて出て来ることになるので、
![]() のセクションがフルに必要になる。
これは面白い事実のような気がする。)
のセクションがフルに必要になる。
これは面白い事実のような気がする。)
もう少し ![]() 多様体の量子化の話を続けると、
考えている多様体が偶数次元の時にスムースな非可換スキームを得るのには、
5 節の4.によれば、
多様体の量子化の話を続けると、
考えている多様体が偶数次元の時にスムースな非可換スキームを得るのには、
5 節の4.によれば、
![]() が非退化な方向に変形するのが良いと思われる。
このような場合の量子化はシンプレクティック量子化と言われて特に良く調べられて
いる。
ところが代数幾何的な状況においては、
が非退化な方向に変形するのが良いと思われる。
このような場合の量子化はシンプレクティック量子化と言われて特に良く調べられて
いる。
ところが代数幾何的な状況においては、![]() が全ての点で
非退化であることを望むのは
一般には不可能である。後述するように、
が全ての点で
非退化であることを望むのは
一般には不可能である。後述するように、![]() が退化している場所では
退化していない所に比べて特異な現象が起こっており、
5 節の2. に
照らしてもあまり嬉しくない。
このことは、ひょっとしたら
が退化している場所では
退化していない所に比べて特異な現象が起こっており、
5 節の2. に
照らしてもあまり嬉しくない。
このことは、ひょっとしたら ![]() が正則な関数であると言う要請が
(多様体の計量が正則関数であると言うのが望みすぎ、と言うのと同様に)
望みすぎであるのではないか、とも思わせる。
しかしこれはこの段階であまり憂慮しても仕方がないというものだろう。
が正則な関数であると言う要請が
(多様体の計量が正則関数であると言うのが望みすぎ、と言うのと同様に)
望みすぎであるのではないか、とも思わせる。
しかしこれはこの段階であまり憂慮しても仕方がないというものだろう。
非可換変形の実現の簡単な例として、接合積による構成を
扱ってみることにする。![]() を
を ![]() 上の可換なプロパー、スムースなスキームとし、
上の可換なプロパー、スムースなスキームとし、
![]() には自己同型の1パラメーター群
には自己同型の1パラメーター群
![]() が与えられているとする。
特に、
が与えられているとする。
特に、![]() 上には ベクトル場
上には ベクトル場 ![]() (
(![]() の無限小生成元
の無限小生成元
![]() )
が一つ与えられていることになる。
)
が一つ与えられていることになる。
![]() 上に
上に ![]() として
として
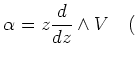
この構成を使えば q-rational/q-ruled な曲面を作ることができる。
ここで ![]() の退化した点で起こる現象について観察してみよう。
の退化した点で起こる現象について観察してみよう。
![]() の各点において
の各点において ![]() は明らかに退化している
(のみならず、完全に 0 である。)
これらの点は変形後も生き残っていて、非可換空間では珍しいはずの
は明らかに退化している
(のみならず、完全に 0 である。)
これらの点は変形後も生き残っていて、非可換空間では珍しいはずの ![]() -値点
を生み出している。すなわち
-値点
を生み出している。すなわち ![]() は交換関係 7.1
の解になっている。
この例に限らず一般的に言って
は交換関係 7.1
の解になっている。
この例に限らず一般的に言って ![]() が 0 になる点では交換関係
の変更後も
が 0 になる点では交換関係
の変更後も![]() -値点が残り、他の部分と明白な相違を見せていて、いわば
「特異な」印象を与える。
逆に言うとこれら
-値点が残り、他の部分と明白な相違を見せていて、いわば
「特異な」印象を与える。
逆に言うとこれら ![]() -点が十分たくさんあるおかげで、そこを「切れ目」に
上の命題で言うところの
-点が十分たくさんあるおかげで、そこを「切れ目」に
上の命題で言うところの
![]() をアファインスキームの和に分割でき、
quasi-scheme たり得ているのであって、そういう切れ目のない対象
(もしあれば-前述のM.Artin の予想は曲面ではそういうものはないことを
主張している)に出食わしたらうまく扱えるかどうか、興味深いところである。
をアファインスキームの和に分割でき、
quasi-scheme たり得ているのであって、そういう切れ目のない対象
(もしあれば-前述のM.Artin の予想は曲面ではそういうものはないことを
主張している)に出食わしたらうまく扱えるかどうか、興味深いところである。