
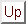


: 可換スキームの非可換スキームとしての無限小変形
: 曲面の非可換変形のいくつかの例について
: 非可換スキームの定義
目次
スキームの定義は前節に述べたようなものがあるので、次の目標は
非特異多様体に当たる「良い」スキームを定義することである。
どのような意味で「良い」かはいろいろ考えられようが、いくつか羅列してみると、
- (コ)ホモロジー論的な定義を考える。
スムース性の最終的な定義は
ホモロジー代数の言葉で述べられるのが妥当であると思われる。
既にいくつか定義が提出されているようであるが、いまのところ
私は余り詳しくないのでここで述べることは控えさせて頂く。
- 非特異性の本質はその等質性にある、と見ることもできる。
例えば、
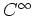 多様体はその自己微分同相群上の等質空間であり、
スムースな可換スキームには自己同型は少ないがその無限小版である
ベクトル場が局所的には十分多くある。
多様体はその自己微分同相群上の等質空間であり、
スムースな可換スキームには自己同型は少ないがその無限小版である
ベクトル場が局所的には十分多くある。
- 良いものの小さい変形はよいはずである。と言う仮設をたてることもできる。
たとえば、通常の意味のスムースなスキームは良いものであろうから、
その小さい変形を考えれば良いスキームの例を作れるのではないか。
(ただし話を「プロパーな」スキームに限るべきである。プロパーでない多様体の
変形はいきなり悪くなる可能性がある。)
- generic なものは良いものである。すなわち、非可換スキームの族において、
大多数を占めるものの特徴が良いものを表現している。
次節以降では、3.の考えに従って、「良い」非可換スキームの例を得ることを
試みよう。
平成15年9月1日