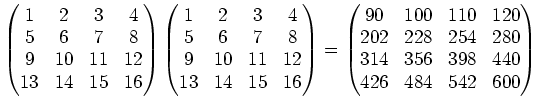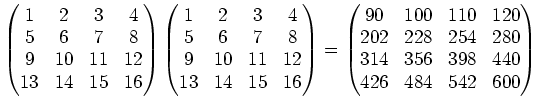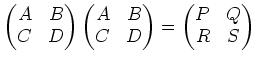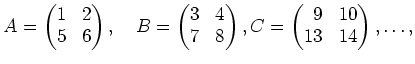

: 行列の積を行列と列ベクトルの積に分解する。
: 行列の計算のテクニック
: 基本ベクトル以外のベクトルへのかけ算
行列の計算はブロック区分けするとわかりやすくなることがしばしばある。
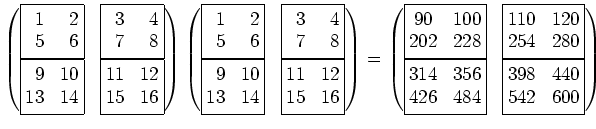
ここで言うブロック区分けとは、たとえば、
という計算を次のように区切ってみる
6。
面倒なので区切った部分を記号でおこう。
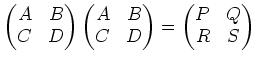 |
(♪) |
ここで
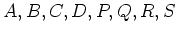 は
は 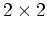 行列で、
という具合ある。
行列で、
という具合ある。
うえのごとく便宜上おいた式(♪)において、あたかも普通の行列のごとく
行列のかけ算をした式
がそのまま成り立っているということが大事なことである。
これは上の例だけでなく、どんな行列を、どのように切っても(ただし
かけ算が意味を持つようにそろえて切る必要がある。)成り立つのであって、
極めて柔軟である。ここでは全てを書ききれない(なにしろ上のごとき行列を
書くのは面倒なのだ。)ので、
是非自分でいろいろと確かめていただきたい。
ただし行列は可換ではないので、その順序にだけは注意を払う必要がある。
平成15年1月30日