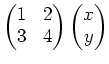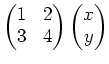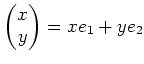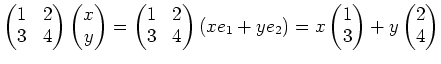

: その2:行列のブロック区分け
: その1:基本列ベクトル
: 前小節の補遺
基本列ベクトルへのかけ算の答えが十分早くわかるようになったら、
(といっても、要するに見たままなわけだが、)
の求め方も少し工夫してみよう。
であるということと、行列算の線型性を用いると、
という具合だ。つまり、行列を列ベクトルに掛けるということは、
基本列ベクトルの行き先(これは、
何度も言うように、行列の列ベクトル)に適当な係数をつけて
足しあわせる(「重ね合わせる」と言ったほうが
イメージがわくかも知れない)ことによって得られるわけだ。
上記のような小さい行列の場合にはどちらで考えても同じようなものであるが、
大きな行列を考える際にはこの考え方がうまくいくことも多い。
平成15年1月30日