Next: general localization of modules Up: , , and the Previous: kernels, cokernels, etc. on
 be a commutative ring. Let
be a commutative ring. Let 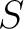 be its subset.
We say that
be its subset.
We say that  is multiplicative if
is multiplicative if
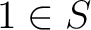

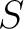 be a multiplicative subset of a commutative ring
be a multiplicative subset of a commutative ring  .
Then we define
.
Then we define ![$A[S^{-1}]$](img317.png) as
as
![$\displaystyle A[\{X_s ; s \in S\}]/(\{ s X_s -1; s \in S\})
$](img318.png)
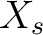 is a indeterminate prepared for each element
is a indeterminate prepared for each element
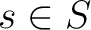 .)
We denote by
.)
We denote by 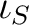 a canonical map
a canonical map
![$A\to A[S^{-1}]$](img322.png) .
.
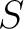 be a multiplicative subset of a commutative ring
be a multiplicative subset of a commutative ring  .
Then the ring
.
Then the ring
![$B=A[S^{-1}]$](img323.png) is characterized by the following
property:
is characterized by the following
property:
Let  be a ring,
be a ring,
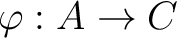 be a ring homomorphism such that
be a ring homomorphism such that
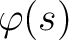 is invertible in
is invertible in  for any
for any 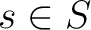 .
Then there exists a unique ring homomorphism
.
Then there exists a unique ring homomorphism
![$\psi=\phi[S^{-1}]:B\to C$](img327.png) such that
such that
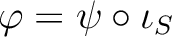
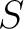 be a multiplicative subset of a commutative ring
be a multiplicative subset of a commutative ring  .
Let
.
Let 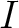 be an ideal of
be an ideal of  given by
given by
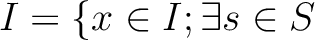 such that
such that 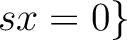
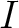 is an ideal of
is an ideal of  .
Let us put
.
Let us put
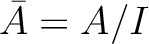 ,
,
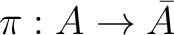 the canonical
projection. Then
the canonical
projection. Then
(2)
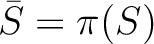 is multiplicatively closed.
is multiplicatively closed.
(3) We have
![$\displaystyle A[S^{-1}]\cong\bar{A}[\bar{S}^{-1}]
$](img334.png)
(4)
![$\iota_{\bar{S}}: \bar{A}\to \bar{A}[\bar{S}^{-1}]$](img335.png) is injective.
is injective.
![$A_f=A[S^{-1}]$](img336.png) for
for
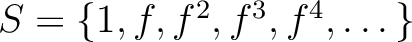 .
The total ring of quotients
.
The total ring of quotients 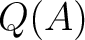 is defined as
is defined as ![$A[S^{-1}]$](img317.png) for
for
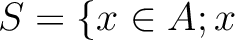 is not a zero divisor of A
is not a zero divisor of A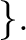
 is an integral domain, then
is an integral domain, then 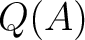 is the field of quotients of
is the field of quotients of  .
.
 be a commutative ring. Let
be a commutative ring. Let
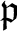 be its prime ideal. Then we define
the localization of
be its prime ideal. Then we define
the localization of  with respect to
with respect to
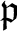 by
by
![$\displaystyle A_\mathfrak{p}=A[ (A\setminus \mathfrak{p})^{-1}]
$](img340.png)