Next: local rings Up: , , and the Previous: general localization of a
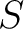 be a multiplicative subset of a commutative ring
be a multiplicative subset of a commutative ring 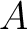 .
Let
.
Let 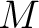 be an
be an 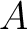 -module
we may define
-module
we may define 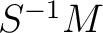 as
as
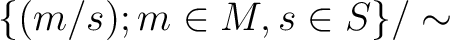
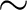 is defined by
is defined by
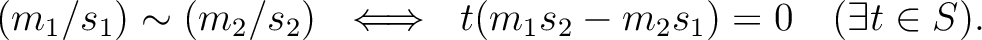
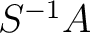 -module structure on
-module structure on 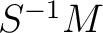 in
an obvious manner.
in
an obvious manner.
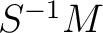 thus constructed satisfies an universality condition which
the reader may easily guess.
thus constructed satisfies an universality condition which
the reader may easily guess.