

Next: S-多項式
Up: グレブナ基底
Previous: 項の辞書式順序
いま、体 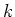 上の多項式環
上の多項式環
![$R=k[X_1,\dots,X_n]$](img26.png) のイデアル
のイデアル
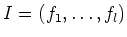 が与えられているとして、
が与えられているとして、
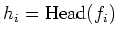 とおくことにする。
とおくことにする。
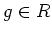 に対して次のような操作を考える 。
に対して次のような操作を考える 。
(操作)
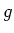 の項のうち
の項のうち 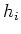 の倍数
の倍数 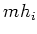 になっているものがあったとする。このとき、
になっているものがあったとする。このとき、
を考える。
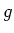 と
と 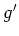 との違いは、
との違いは、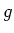 の
の 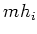 の項がそれより小さい項の和
(
の項がそれより小さい項の和
(
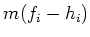 )で置き換わっているところである。
今度は
)で置き換わっているところである。
今度は 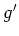 についてこの操作をおこなって
についてこの操作をおこなって 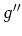 を計算し、...というぐあいに
この操作を繰り返すと有限回で
を計算し、...というぐあいに
この操作を繰り返すと有限回で
に入る元が得られる。
その結果得られた 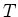 の元を「
の元を「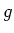 を
を
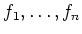 の割った余り」とよぶ。
「割り算」の結果はつぎのように整理することができる。
の割った余り」とよぶ。
「割り算」の結果はつぎのように整理することができる。
ここで、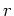 は「余り」で、
は「余り」で、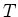 の元。
の元。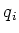 は「商」にあたるもので、
は「商」にあたるもので、
がなりたっている。
上記の 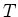 は
は 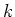 上のベクトル空間であり、
さらに上の説明によって
上のベクトル空間であり、
さらに上の説明によって
であることがわかる。
そこで 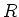 の元を上の式のように
の元を上の式のように 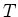 の元と
の元と 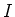 の元に分けるのが、「割り算」
の基本的な考え方である。問題はそのような分け方の一意性にある。
の元に分けるのが、「割り算」
の基本的な考え方である。問題はそのような分け方の一意性にある。
Yoshifumi Tsuchimoto
2001-05-24
![]() に対して次のような操作を考える 。
に対して次のような操作を考える 。
![]() の項のうち
の項のうち ![]() の倍数
の倍数 ![]() になっているものがあったとする。このとき、
になっているものがあったとする。このとき、
![]() と
と ![]() との違いは、
との違いは、![]() の
の ![]() の項がそれより小さい項の和
(
の項がそれより小さい項の和
(
![]() )で置き換わっているところである。
今度は
)で置き換わっているところである。
今度は ![]() についてこの操作をおこなって
についてこの操作をおこなって ![]() を計算し、...というぐあいに
この操作を繰り返すと有限回で
を計算し、...というぐあいに
この操作を繰り返すと有限回で
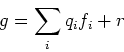
![]() は
は ![]() 上のベクトル空間であり、
さらに上の説明によって
上のベクトル空間であり、
さらに上の説明によって