Next: Zariski topology on affine Up: localization of a commutative Previous: localization of a commutative
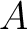 be a ring. If
be a ring. If 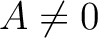 (which is equivalent to saying that
(which is equivalent to saying that
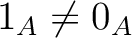 ), then we have
), then we have
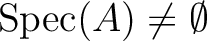 .
.
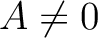 .
Then by Zorn's lemma we always have a maximal ideal
.
Then by Zorn's lemma we always have a maximal ideal
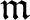 of
of 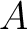 .
A maximal ideal is a prime ideal of
.
A maximal ideal is a prime ideal of 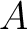 and is therefore an element of
and is therefore an element of
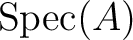 .
.
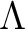
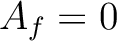 if and only if
if and only if 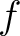 is nilpotent.
(Corollary 7.9).
Since
is nilpotent.
(Corollary 7.9).
Since 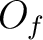 is homeomorphic to
is homeomorphic to
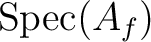 , we have the desired result.
, we have the desired result.