Next: Bibliography Previous: direct image of a
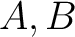 be rings. Let
be rings. Let
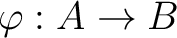 be a ring homomorphism.
We have already introduced
be a ring homomorphism.
We have already introduced
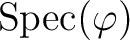 as a continuous map
as a continuous map
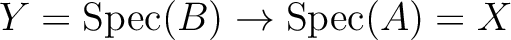 . Now that the spaces
. Now that the spaces
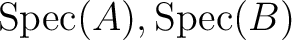 carry
structures of locally ringed spaces, we (re)define
carry
structures of locally ringed spaces, we (re)define
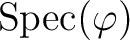 as a morphism of locally ringed spaces by defining
as a morphism of locally ringed spaces by defining
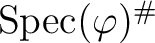 as in Example 9.11.
as in Example 9.11.
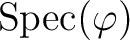 is indeed a morphism of locally ringed space.
is indeed a morphism of locally ringed space.
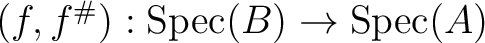 be a morphism of locally ringed space.
Then there exists an unique ring homomorphism
be a morphism of locally ringed space.
Then there exists an unique ring homomorphism
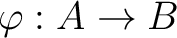 such that
such that
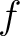 coincides with
coincides with
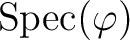 .
.
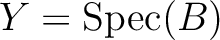 and
and
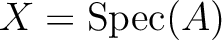 . The data
. The data
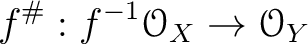
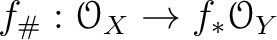
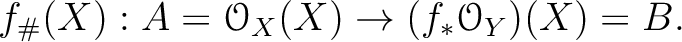
 .
.
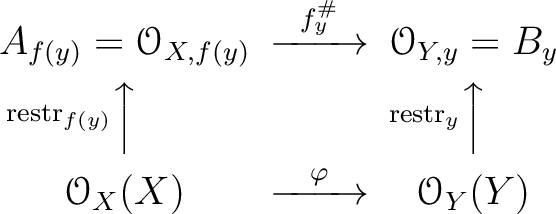
By the hypothesis of 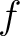 being a morphism of locally ringed spaces,
being a morphism of locally ringed spaces,
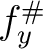 is local homomorphism.
That means,
is local homomorphism.
That means,
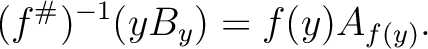
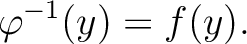
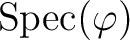 , we have
, we have
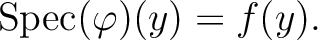
We have thus proved that
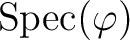 is equal to
is equal to 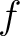 as a map
as a map 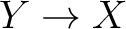 .
.