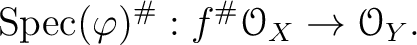Next: Affine schemes and rings: Up: tensor products and inverse Previous: sheaves associated to modules
 be topological spaces.
Let
be topological spaces.
Let 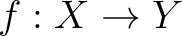 be a continuous map.
Let
be a continuous map.
Let
 be a sheaf on
be a sheaf on 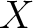 . Then we define its direct image
with respect to
. Then we define its direct image
with respect to 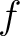 by
by
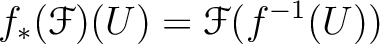
 be topological spaces.
Let
be topological spaces.
Let 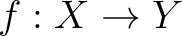 be a continuous map.
Let
be a continuous map.
Let
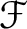 be a sheaf on
be a sheaf on 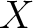 .
Let
.
Let
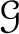 be a sheaf on
be a sheaf on 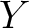 .
Then we have a natural isomorphism.
.
Then we have a natural isomorphism.
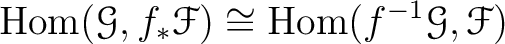
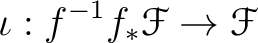
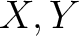 be (locally) ringed spaces.
Let
be (locally) ringed spaces.
Let 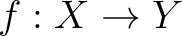 be a morphism of (locally) ringed spaces.
Let
be a morphism of (locally) ringed spaces.
Let
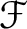 be a sheaf of
be a sheaf of
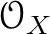 -modules.
Let
-modules.
Let
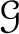 be a sheaf on
be a sheaf on
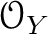 -modules.
Then we have a natural isomorphism of modules.
-modules.
Then we have a natural isomorphism of modules.
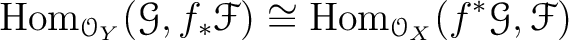
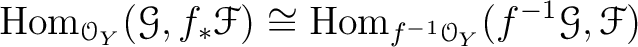 | ||
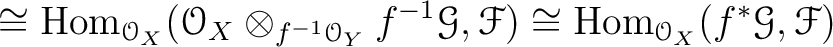 |
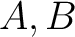 be rings. Let
be rings. Let
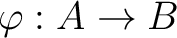 be a ring homomorphism.
We put
be a ring homomorphism.
We put
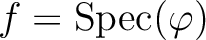 be the continuous map
be the continuous map
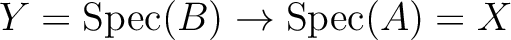 corresponding to
corresponding to  .
We note that
.
We note that 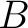 carries an
carries an  -module structure via
-module structure via 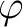 .
Accordingly, we have the corresponding sheaf
.
Accordingly, we have the corresponding sheaf
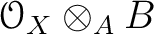 on
on 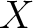 .
We may easily see that this sheaf coincides with
.
We may easily see that this sheaf coincides with
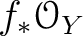 .
The map
.
The map
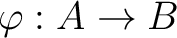 then may also be regarded as a homomorphism of
then may also be regarded as a homomorphism of  -modules.
We have thus an
-modules.
We have thus an
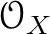 module homomorphism
module homomorphism
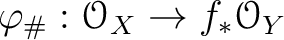
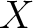 .
By the adjoint relation (Proposition 9.9),
we obtain a sheaf homomorphism
.
By the adjoint relation (Proposition 9.9),
we obtain a sheaf homomorphism