localization of a commutative ring

.

DEFINITION 04.2   Let $f$ be an element of a commutative ring $A$ . Then we define the localization $A_f$ of $A$ with respect to $f$ as a ring defined by

$$A_{f}=A[X]/(X f -1)$$

where $X$ is a indeterminate.

In the ring $A_f$ , the residue class of $X$ plays the role of the inverse of $f$ . Therefore, we may write $A[1/f]$ instead of $A_f$ if there is no confusion.

One may define localization in much more general situation. The reader is advised to read standard books on commutative algebras.

LEMMA 04.3   Let $f$ be an element of a commutative ring $A$ . Then there is a canonically defined homeomorphism between $O_f$ and $\operatorname{Spec}(A_f)$ . (It is usual to identify these two via this homeomorphism.)

PROOF.. Let $i_f:A \to A_f$ be the natural homomorphism. We have already seen that we have a continuous map

$$\operatorname{Spec}(i_f):\operatorname{Spec}(A_f)\to \operatorname{Spec}(A).$$

We need to show that it is injective, and that it gives a homeomorphism between $\operatorname{Spec}(A_f)$ and $O_f$ .

Let us do this by considering representations.

1. $\mathfrak{p}\in \operatorname{Spec}(A)$ corresponds to a representation $\rho_\mathfrak{p}$ .

2. $\mathfrak{q}\in \operatorname{Spec}(A_f)$ corresponds to a representation $\rho_\mathfrak{q}$ .

3. $\operatorname{Spec}(i_f)$ corresponds to a restriction map $\rho\mapsto \rho \circ i_f$ .

Now, for any $\mathfrak{p}\in \operatorname{Spec}(A)$ , $\rho_\mathfrak{p}$ extends to $A_f$ if and only if the image $\rho_\mathfrak{p}(f)$ of $f$ is invertible, that means, $\rho_\mathfrak{p}(f)\neq 0$ . In such a case, the extension is unique. (We recall the fact that the inverse of an element of a field is unique.)

It is easy to prove that $\operatorname{Spec}(i_f)$ is a homeomorphism. $\qedsymbol$

Let $A$ be a ring. Let $f\in A$ . It is important to note that each element of $A_f$ is written as a ``fraction''

$$\frac{x}{f^k} \qquad (x\in A; k\in \mathbb{N}).$$

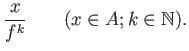
One may introduce $A_f$ as a set of such formal fractions which satisfy ordinary computation rules. In precise, we have the following Lemma.

LEMMA 04.4   Let $A$ be a ring, $f$ be its element. Let us consider the following set

$$S=\{ (x ,f^k); x\in A; k\in \mathbb{N}\}.$$

We introduce on $S$ the following equivalence law.

$$(x ,f^k) \sim (y,f^l) \iff (y f^k-x f^l)f^N=0 \qquad (\exists N\in \mathbb{N})$$

Then we may obtain a ring structure on $S/\sim$ by introducing the following sum and product.

$$(x /f^k) + (y/f^l)=(x f^l +y f^k/ f^{k+l})$$

$$(x /f^k) (y/f^l)=(x y / f^{k+l})$$

where we have denoted by $(x/f^k)$ the equivalence class of $(x,f^k)\in S$ .

COROLLARY 04.5   Let $A$ be a ring, $f$ be its element. Then we have $A_f=0$ if and only if $f$ is nilpotent.

Likewise, for any $A$ -module $M$ , we may define $M_f$ as a set of formal fractions

$$\frac{m}{f^k} \qquad (m\in M; k\in \mathbb{N}).$$

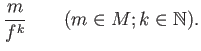
which satisfy certain computation rules.