-
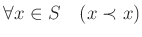
-
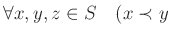 and
and 
以下、小さい字で妖精国での対応物を書く。
![]() には、次のような前順序関係が入る。
には、次のような前順序関係が入る。
![]() に同値関係
に同値関係 ![]() が、
が、
で定義される。
![]() とは、
とは、 ![]() が
が ![]() の親戚であるということである
の親戚であるということである
同値関係により、![]() がクラス分けされる。
各クラスは「親族」である
がクラス分けされる。
各クラスは「親族」である
クラス
![]() ごとに
ごとに
![]() から
から ![]() への写像
への写像 ![]() とその逆写像
とその逆写像 ![]() を組み立てよう。
2つのケースに分かれる。
を組み立てよう。
2つのケースに分かれる。
Case I: ![]() に最小元がない場合。
に最小元がない場合。
このばあい、
![]() である。
である。
と取れば良い。
Case II. ![]() に最小元がある場合。
に最小元がある場合。
その最小元を ![]() とおこう。
とおこう。
![]() は互いに相異なる。
は互いに相異なる。
すなわち、
![]() なのである。
なのである。
![]() だったから、
だったから、
![]()
![]() .
.
![]() か否かによってふたとおりに場合分けされる。
か否かによってふたとおりに場合分けされる。
Case II-1).
![]() のとき。
のとき。
![]() である。
である。
従って、Case I と同じく
と取れば良い。
Case II-2).
![]() のとき。
のとき。
このときのみ、![]() と
と
![]() の間に違いが生じる。
の間に違いが生じる。
![]() と
と
![]() との全単射を与えるには、一つずらせば良い。
との全単射を与えるには、一つずらせば良い。
は全単射であって、その逆写像を
と取れば良い。
上の証明は クラス分けの際に 選択公理を使っている。 実際には、選択公理を使わなくても済むので、 これは少し「弱み」と言えるかもしれない。
選択公理を使わずに証明するには、次のように考える。
![]() とおく。
とおく。
![]() は へそのない最長老たちの全体の集合にあたる。
は へそのない最長老たちの全体の集合にあたる。
さらに、
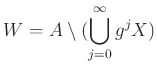
とおこう。 [
さて、
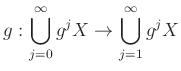
は全単射である。
次のことは容易に分かる。
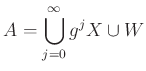
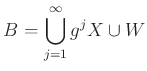
よって、
このラインが、 本講義の教科書(小林、逸見著、「集合と位相空間の基礎、基本」)にある証明 である。記号もなるべくあわせてある。詳細は教科書を参照のこと。