- For any
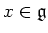 and for any
and for any
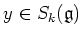 ,
,
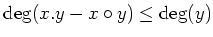
- If
 ,
then we have
,
then we have
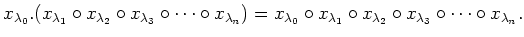
- For any
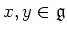 and for any
and for any
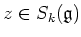 , we have
, we have
![$\displaystyle x.(y.z)-y.(x.z)=[x,y].z
$](img34.png)
which obeys the following rules:
as a
We define inductively the action of
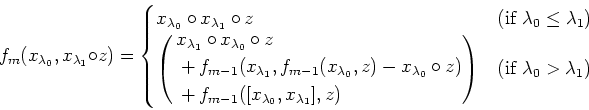
We first note that the above definition is necessary to meet our conditions.
Indeed, by (2) we necessarily define as above for
![]() .
When
.
When
![]() , we compute
, we compute
It is easy to see that the conditions (1),(2) are satisfied by ![]() defined as
above..
Let us proceed to verify that the
defined as
above..
Let us proceed to verify that the ![]() so defined also satisfies (3).
Let us consider
so defined also satisfies (3).
Let us consider
![]()
![]() with
with
![]() ,
, ![]() .
We need to prove
.
We need to prove
(i) Case where
![]() .
.
On the other hand we have
(ii) Case where
![]() .
.
In this case we need to ``decompose'' ![]() further:
further:
We first forget about the hypothesis
Let us now admit that the above equation
![]() is true and prove the rest of
the equation (3). By interchanging
is true and prove the rest of
the equation (3). By interchanging ![]() and
and ![]() in
the equation (
in
the equation (
![]() ), we obtain
), we obtain
It remains to prove the equation (
![]() ).
By the induction hypothesis we have
).
By the induction hypothesis we have
Also by the induction hypothesis we have
Lastly, we decompose ![]() as
as
Then the second term
These altogether complete the proof.
be the obvious
Using the universality of symmetric algebra,
there exists a unique ![]() -algebra homomorphism
-algebra homomorphism
which extends
which is clearly degree-decreasing. So it defines a
Now the composition we obtain
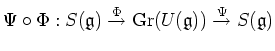
coincides with the identity map. Indeed, it coincides with the identity on monomials of the form
The map ![]() is easily verified to be surjective. So we conclude that
is easily verified to be surjective. So we conclude that ![]() and
and ![]() are both bijective and are inverse to each other.
are both bijective and are inverse to each other.
![]()