which satisfies the following axioms:
![$ [X,X]=0 $](img7.png) for all
for all
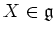 .
.
- (``Jacobi identity'')
![$\displaystyle [X,[Y,Z]] =[[X,Y],Z]]+[Y,[X,Z]] \qquad (\forall X,Y,Z\in \mathfrak{g}).
$](img9.png)
which satisfies the following axioms:
with the following universal property:
For any associative unital algebra ![]() with a Lie algebra homomorphism
with a Lie algebra homomorphism
![]() , there exists a unique algebra homomorphism
, there exists a unique algebra homomorphism
such that
The pair
![]() is unique up to an isomorphism.
is unique up to an isomorphism.
Universal enveloping algebras of Lie algebras form an important class of non commutative associative algebras. Our task in this Part is to describe these algebras in our language.