EXAMPLE 5.45
Let
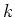
be a field of characteristic
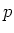
(possibly 0
).
is a Lie algebra with the Killing form
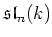 is an ideal of
is an ideal of
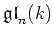 and so its Killing form is given by
and so its Killing form is given by
If
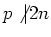
, then the Killing form is easily seen to be non-degenerate.
so
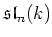
is a non-degenerated Lie algebra in this case. In this
way we see that it is a semisimple Lie algebra. The Lie algebra
is actually simple as we have shown in
Proposition
5.22.
EXAMPLE 5.46
Let
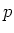
be an odd prime.
Let
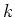
be a field of characteristic
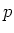
.
Then we have shown in Proposition
5.19
that the only non trivial ideals of
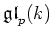
are
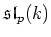
and
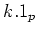
.
So we see that
is a semisimple Lie algebra (as it has no proper abelian ideals).
It has a unique nontrivial ideal
Thus
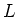
cannot be a direct sum of simple Lie algebras.
![]() is an ideal of
is an ideal of
![]() and so its Killing form is given by
and so its Killing form is given by
![]() is an ideal of
is an ideal of
![]() and so its Killing form is given by
and so its Killing form is given by