

Next: Ideals of .
Up: generalities in finite dimensional
Previous: Theorem of Engel
Recall that
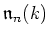 denotes the Lie algebra of strictly upper triangular
matrices. In this subsection we denote by
denotes the Lie algebra of strictly upper triangular
matrices. In this subsection we denote by 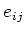 the elementary matrices.
(as we have done so without even mentioning...)
the elementary matrices.
(as we have done so without even mentioning...)
PROOF..
Let us denote by
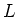
the left hand side of the lemma.
Then we trivially have
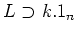
.
Furthermore, for all
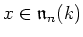
, we see easily that
holds. So we have
Let us prove the opposite inclusion.
We take an arbitrary element 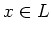 .
.
For any 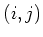 satisfying
satisfying 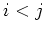 ,
we have
,
we have
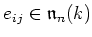 and thus
and thus
The rank of the left hand side is at most
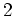
. So
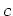
must be equal to 0
when
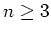
.
Otherwise (
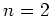
), we compare the trace of the both
hand sides. The trace of the left hand side is clearly zero.
The trace of a scalar matrix
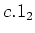
is equal to
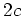
. Thus
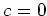
by our assumption (
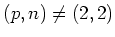
).
In either case, we have
![$ [e_{i,j},x]=0$](img282.png)
.
Then we compute some of special cases.
First, let us examine the case where
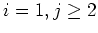
. Then
By looking at
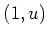
entry of the above equation,
we conclude that equations in entries
hold.
Similarly, by looking at the
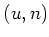
entry of
![$ [e_{i n},x]$](img289.png)
,
we conclude that equations
hold.
Putting the equations all together, we conclude that
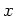
is in the right
hand side of the lemma.
As an application of the Engel's theorem, we prove the following proposition.
PROPOSITION 5.19
Let 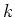 be a field of characteristic
be a field of characteristic 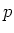 (possibly 0
).
Let
(possibly 0
).
Let 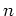 be a positive integer.
We assume that
be a positive integer.
We assume that
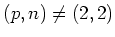 .
Then each ideal
.
Then each ideal 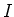 of
of
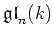 is equal to the one in the following list.
is equal to the one in the following list.
- 0
.
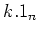 .
.
-
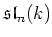 .
.
-
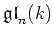 .
.
PROOF..
The case
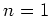
is trivial. So let us assume
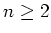
.
If
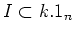 , then
, then
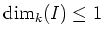 and hence
and hence 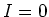 or
or 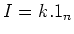 .
Assume now
.
Assume now
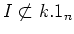 .
Let us consider the Lie algebra
.
Let us consider the Lie algebra
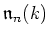 of strictly upper triangular matrices.
Then
of strictly upper triangular matrices.
Then
satisfies the assumption of the Engel's theorem.
So there exists a non-constant element
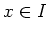
such that
holds.
By using the previous lemma, we see that
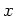
may be presented as
Since
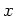
is non-constant, we have
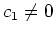
.
Thus
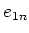
belongs to
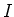
.
By changing the order of the base and repeating the
above argument, we conclude that
In addition we have
This clearly proves
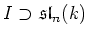
.
Since the codimension of
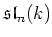
in
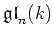
is
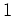
, we have
either
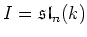
or
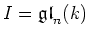
.
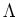
For the sake of completeness, we deal with the case
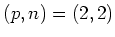 .
In this case, situation is a bit different.
.
In this case, situation is a bit different.
PROOF..
(1)
There exists a traceless non constant matrix
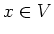
such
that
holds.
By subtracting a constant matrix, one may easily replace
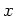
by a matrix
with zero diagonals.
(2) By a direct computation we see
(Note that
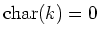
.)
(3)
![$ \mathfrak{t}_2(k)=L_{[1:0]}$](img326.png) .
.
PROPOSITION 5.21
Let 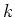 be a field of characteristic
be a field of characteristic 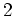 . Then each ideal
. Then each ideal 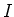 of
of
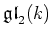 is equal
to the one in the following list.
is equal
to the one in the following list.
- 0
.
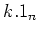 .
.
- A two-dimensional Lie algebra
![$ L_{[b:c]}$](img317.png) defined as in the lemma above.
defined as in the lemma above.
-
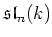 .
.
-
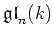 .
.
PROOF..
We divide into several cases.
(i)
Case where
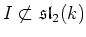 .
In this case there exists an element
.
In this case there exists an element 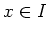 with
with
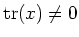 .
Putting
.
Putting
we compute as follows
(Note
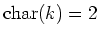
.)
Then we have
Thus we see that
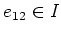
.
In a same way (by changing the order of the base), we obtain,
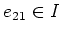
.
Since
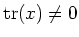
, we see that
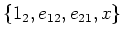
spans the
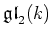
.
thus
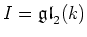
in this case.
(ii)
Case where
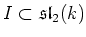 and
and
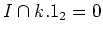 .
Let
.
Let 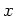 be arbitrary element of
be arbitrary element of 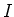 and put
and put
Then by computing
![$ [e_{1 2},x]$](img341.png)
as
in the case (i) above, we know that
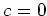
. Similarly, we know
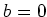
.
Since
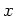
is traceless,
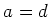
also holds.
So the only possibility in this case is
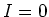
.
(iii)
Case where
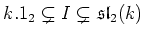 .
By a dimension consideration, we see that
.
By a dimension consideration, we see that 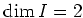 .
Then we use the above lemma.
.
Then we use the above lemma.
(iv)
The case 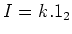 or
or
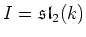 .
Excellent. There is nothing to in this case.
.
Excellent. There is nothing to in this case.


Next: Ideals of .
Up: generalities in finite dimensional
Previous: Theorem of Engel
2007-12-19
![]() .
.
![]() satisfying
satisfying ![]() ,
we have
,
we have
![]() and thus
and thus
![$\displaystyle 0=[e_{1 j}, x]= \sum_{s t} [e_{1 j}, x_{s t} e_{s t}] = \sum_{t } x_{j t} e_{1 t} -\sum_s x_{s 1} e_{s j}$](img284.png)
![]() , then
, then
![]() and hence
and hence ![]() or
or ![]() .
Assume now
.
Assume now
![]() .
Let us consider the Lie algebra
.
Let us consider the Lie algebra
![]() of strictly upper triangular matrices.
Then
of strictly upper triangular matrices.
Then
![]()
![]() .
In this case, situation is a bit different.
.
In this case, situation is a bit different.
![$\displaystyle L_{[b:c]}
=k. 1_n + k.
\begin{pmatrix}
0& b \\
c & 0
\end{pmatrix}.
$](img319.png)
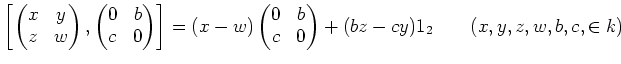
![]() .
.
![]()
![]() .
In this case there exists an element
.
In this case there exists an element ![]() with
with
![]() .
Putting
.
Putting
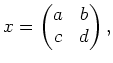
![$\displaystyle I\ni
[e_{1 2}, x]
=\left[
\begin{pmatrix}
0& 1 \\
0 & 0
\end{pm...
...
c & d
\end{pmatrix}\right]
=
\begin{pmatrix}
c& a+d \\
0 & c
\end{pmatrix}.
$](img330.png)
![$\displaystyle I \ni
[e_{1 1},[e_{1 2},x]]
=
\left[
\begin{pmatrix}
1& 0 \\
0 &...
...\\
0 & c
\end{pmatrix}\right]
=
\begin{pmatrix}
0& a+d \\
0 & 0
\end{pmatrix}$](img332.png)
![]() and
and
![]() .
Let
.
Let ![]() be arbitrary element of
be arbitrary element of ![]() and put
and put
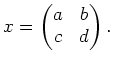
![]() .
By a dimension consideration, we see that
.
By a dimension consideration, we see that ![]() .
Then we use the above lemma.
.
Then we use the above lemma.
![]() or
or
![]() .
Excellent. There is nothing to in this case.
.
Excellent. There is nothing to in this case.
![]()