In this section, we always assume ![]() to be a prime number.
to be a prime number.
be a connection with zero curvature. Then the
From the argument of the previous section we see that the p-curvature is
![]() -linear.
-linear.
A fairly good account on ![]() -curvatures is given in [2].
Our treatment here is a bit different.
It is not so general, but is easy using only
arguments on rings and modules.
-curvatures is given in [2].
Our treatment here is a bit different.
It is not so general, but is easy using only
arguments on rings and modules.
be a connection on
of parallel sections as a
![]() is said to be locally generated by parallel sections
if there exists
an open covering
is said to be locally generated by parallel sections
if there exists
an open covering
![]() of
of ![]() such that
such that
![]() is
generated by parallel sections.
is
generated by parallel sections.
be a connection on
Then the following conditions are equivalent.
Since the question is local, we may reduce the proposition to an
lemma which we describe later.
Before we do that, we need some preparation.
First we note that when ![]() is smooth of relative dimension
is smooth of relative dimension ![]() ,
we may locally choose a set of elements
,
we may locally choose a set of elements
![]() (``coordinates'') such that
(``coordinates'') such that
![]() is freely generated by
is freely generated by
![]() over
over
![]() .
Let
.
Let ![]() be an affine open subset of
be an affine open subset of ![]() on which such a local coordinate
system exists. Then there exists vector fields
on which such a local coordinate
system exists. Then there exists vector fields
on
Note also that from this observation we see
Next, let us set some more notation. We employ the graded lexicographic order on an index set
We define an order reversing map
Finally, for any
![]() , we define
, we define ![]() by
by
be a connection on
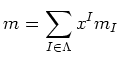
holds.
Since we know that curvature is
![]() : obvious.
: obvious.
![]() :
For any
:
For any
![]() and for any
and for any ![]() , we put
, we put
Note that the condition (1) tells us that
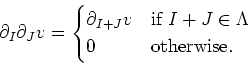
Now we claim :
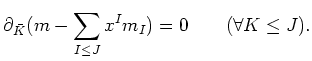
So it is enough to put
Assume now that the claim holds for all ![]() .
Since
.
Since ![]() is well-ordered set, there exists an index
is well-ordered set, there exists an index ![]() which is just before
which is just before ![]() . (That means,
. (That means,
![]() is the largest index which is smaller than
is the largest index which is smaller than ![]() .)
.)
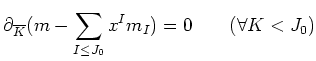
Let us put
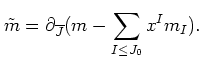
Then for any
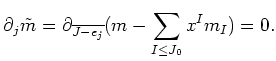
Thus we have
Then we put
We may easily see that
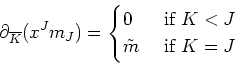
holds and thus the claim holds for
It is worthwhile to note that the coefficients ![]() in the condition (3)
of the Lemma above is unique. Namely,
in the condition (3)
of the Lemma above is unique. Namely,
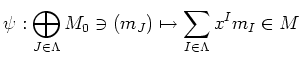
is bijective.
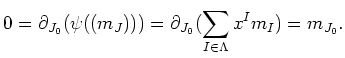
This contradicts the assumption.
![]()
Then every element
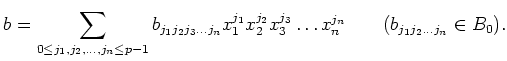
To obtain that, first we recall Taylor expansion
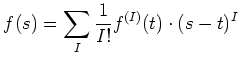
of a polynomial
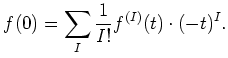
By analogy we put
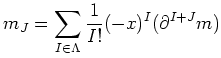
Then we see that
Indeed, we have the following lemma.
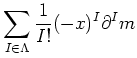
is parallel.
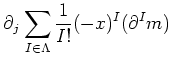 | ||
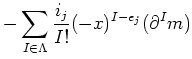 | ||
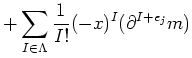 | ||
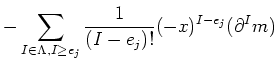 | ||
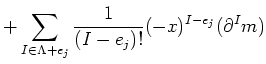 |
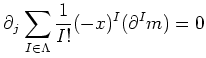
as required.
![]()
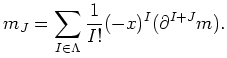
Then:
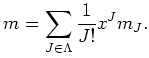
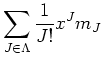 | ||
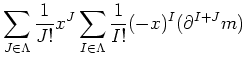 | ||
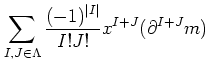 | ||
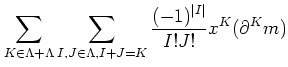 |
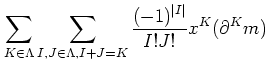 | ||
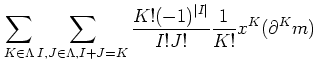 |
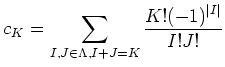 |
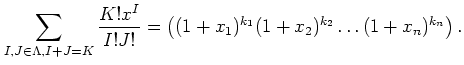 |
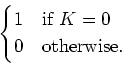 |