``Universal representation" of Weyl algebras and derivations

LEMMA 8.1   Let $k$ be a field of characteristic $p\neq 0$ . Let $t_1,t_2,\dots,t_{2n}$ be indeterminates over $k$ . Then we have an injection

$$\Phi:A_n(k)\to M_{p^n}(k[t_1,t_2,\dots,t_{2n}])$$

such that

$$\Phi(\gamma_i)=\mu_i+t_i.$$

PROOF.. We first note that $\Phi(\gamma_i^p)=t_i^p$ holds for all $i$ . Thus for any element $x\in A_n(k)$ , we write

$$x=\sum_I \gamma^I p_I(\gamma_1^p,\gamma_2^p,\gamma_3^p,\dots,\gamma_{2n}^p)$$

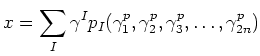
where sum is taken over multi-indices $I\subset \{0,1,2,3,\dots,p-1\}^n$ . Then we obtain

$$\Phi(x)= \sum_I (\mu+t)^I p_I(t_1^p,t_2^p,t_3^p,\dots,t_{2n}^p)$$

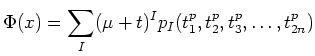
Now, let $I_0$ be the greatest index among $I$ such that $p_I\neq 0$ (in lexicographical order). Then we have

$$\partial_{I_0} \Phi(x)=(I_0!)p_I(t^p)\neq 0.$$

This is contrary to the assumption that $\Phi(x)=0$ . Thus we have $p_I=0$ for all $I$ . $\qedsymbol$

The representation is ``universal". It contains all the information of $A_n(k)$ and also carries all the irreducible finite-dimensional representations as specializations.

Via this representation, any element of $A_n(k)$ may be viewed as a matrix-valued polynomial function on the affine space $\mathbb{A}^{2 n}$ .