


: この文書について...
代数学演習 I 問題 No.9

今回も「環」といえば単位元を持つ可換環であるとし、「環の準同型」は
単位元を保つものだけを考えることにします。
定義 9.1
整域
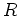
が一意分解環(unique factorization domain:UFD) であるとは、
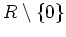
の任意の元
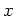
が素元の積に
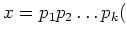
$p_1,...,p_k$ は $R$ の素元
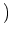
のように書けるときに言います。
(
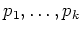
の中には同じものがあってもよい。)
定義 9.2
整域
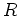
が 単項イデアル整域 (principal ideal domain:PID) であるとは、
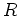
のすべてのイデアルが単項イデアル(一つの元で生成されるイデアル)であるときに言います。
これから暫くの間 (3回ぐらい)上の3つのタイプの環が主題になります。基本的には、
ED
PID
UFD
例題 9.1 (整列集合の定義の確認)
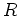
をユークリッド整域とし、
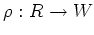
を定義
9.3 に出てくる写像とします。この時、任意の
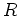
の部分集合
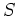
に対して、
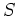
の中で重さが最小のもの(「一番軽いもの」)があることを示しなさい。
「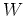 が整列集合である」とは、「
が整列集合である」とは、「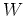 の任意の部分集合
の任意の部分集合 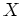 は最小元を持つ」ということでした。そこで、「
は最小元を持つ」ということでした。そこで、「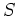 の元の重さの集合」
を
の元の重さの集合」
を 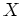 として採用すると、この中に最小元がある筈です。これを
として採用すると、この中に最小元がある筈です。これを 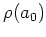 とすれば、
とすれば、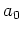 が求めるものということになります。(注意:一番軽い元は一つとは限りません。)
が求めるものということになります。(注意:一番軽い元は一つとは限りません。)
問題 9.2
ユークリッド整域は単項イデアル整域であることを示しなさい。(ヒント:
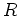
をユークリッド整域とし、
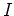
をそのイデアルの一つとします。
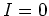
なら単項 (0 で生成される)のでよい。
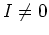
なら、
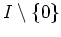
の元のうち、一番軽い元をとってみなさい。)
問題 9.3
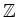
はユークリッド整域であることを、定義に沿って示しなさい。
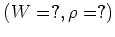
問題 9.4
体
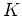
上の一変数多項式環
![$ K[X]$](img35.png)
はユークリッド整域であることを、定義に沿って示しなさい。
問題 9.5
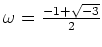
(1の三乗根の一つ)とするとき、
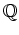
![$ [\omega]$](img38.png)
は体であることを示しなさい。
問題 9.6
![% latex2html id marker 1102
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{-1}]$](img39.png)
は「重み関数」
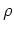
を
で定義することにより、ユークリッド環となることを示しなさい。(ヒント:
![% latex2html id marker 1114
$ \alpha,\beta \in {\mbox{${\mathbb{Z}}$}}[\sqrt{-1}], \beta \neq 0$](img48.png)
とするとき、
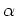
を
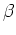
で割った商を求めるには、
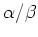
を
![% latex2html id marker 1122
$ {\mbox{${\mathbb{Z}}$}}[\sqrt{-1}]$](img52.png)
の元で近似してみなさい。)
問題 9.8
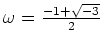
(
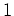
の三乗根の一つ) とします。このとき、
![$ {\mbox{${\mathbb{Z}}$}}[\omega]$](img65.png)
はユークリッド環であることを示しなさい。



: この文書について...
平成17年12月13日
![]()