


: この文書について...
代数学II 要約 No.4
今日のテーマ

前回のレポートで左右の区別ができていなかった答案が目だったので、
ここではっきりさせておこう。ただし、本講義では主に左剰余類を扱う。
命題 4.1
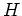
による右クラス分けと左クラス分けが一致するのは、
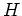
が
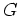
の
正規部分群のときで、その時に限る。
その他に、レポートでは部分群でないものによるクラス分けを試みていたものが
あった。それは大抵うまく行かない。問題 4.1を参照のこと。
準同型定理の話に戻る。次の定理は準同型定理の基本応用例である。
定理 4.2
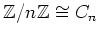
問題 4.1
群
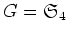
の部分集合
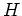
を
で定義する。このとき、
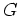
の
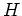
によるクラス分けを定義
4.1 のように
行えるだろうか。うまく行なえないときにはどうしてだめなのか
反例を挙げて答えなさい。
平成16年5月10日
![]()