


: この文書について...
代数学II要約 No.11
今日のテーマ:
![\fbox{
群環 ${\mathbb {C}}[G]$ の環としての構造
}](img1.png)
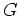 の表現を全て求めるための決定打が、次の定理だ。
の表現を全て求めるための決定打が、次の定理だ。
![$ {\mathbb{C}}[G]$](img3.png) を中心元による固有分解することによって、上の定理は次の
命題に帰着される。
を中心元による固有分解することによって、上の定理は次の
命題に帰着される。
命題 11.2
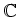
上の有限次元環
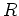
が、
-
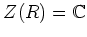
- 全ての左
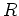 -加群は完全可約である。
-加群は完全可約である。
という条件を満たせば、
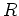
はあるサイズの全行列環
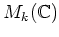
と同型になる。
実は、命題11.2の(2)の仮定のもとでは、
中心元による固有分解は、両側イデアルによる分解でもある。
それが次の補題である。
補題 11.1
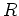
が命題
11.2の(2)を満たすとき、
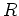
の任意の(両側)イデアル
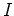
に対して、
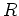
のある(両側)イデアル
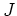
が存在して、
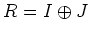
がなりたつ。
とくに、
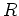
が命題
11.2の条件(1),(2)をともに満たせば、
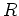
には非自明な
(両側)イデアルが存在しない。
命題11.2の証明にはその他に以下の補題を用いる。
ポイントは、抽象的な条件式(1),(2)からいかにして基本行列 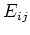 に
該当するものを見つけ出してくるかというところにある。
に
該当するものを見つけ出してくるかというところにある。
補題 11.2
環
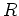
の左イデアル
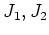
があって、
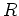
が(
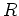
-左加群として)
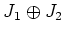
と等しいならば、
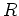
の元
で、
次の条件を満たすものが唯一つ存在する。
-
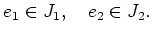
-
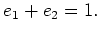
-
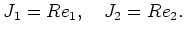
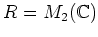 に対して、
に対して、
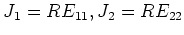 というのが
上の補題の代表的な例である。
というのが
上の補題の代表的な例である。
以下、さらに細かく基本行列を作り出すことになる。
それらの証明はどれも面白いのだが、
細かい話になるし、詳細を知りたい人はむしろ自力で考えた方が良いので、
すべて演習問題にまわすことにする。
まず、
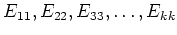 にあたるものを作り出す。
にあたるものを作り出す。
補題 11.3
命題
11.2の仮定のもとで、
-
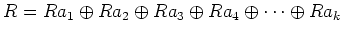 かつ
各
かつ
各 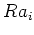 は既約左
は既約左
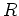 -加群であるような
-加群であるような
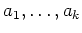 が存在する。
が存在する。
- さらに、
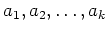 は
は
を満たすように選べる。
-
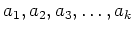 を上のように選んでおくと、
が成り立つ。(ただし
を上のように選んでおくと、
が成り立つ。(ただし
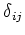 はクロネッカのデルタ。)
はクロネッカのデルタ。)
補題 11.4
上記補題の仮定の元で、
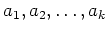
を(1) および(2)が成り立つように
選んでおくと、
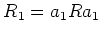
は環になり、しかも非自明な
左イデアル(
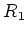
の
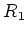
-部分加群)をもたない。
補題 11.5
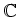
上有限次元の環
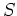
が、非自明な左イデアルをもたないならば、
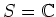
である。特に、補題
11.4の
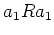
は
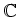
に一致する。
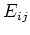 にあたるものを作り出すのが問題11.7である。
にあたるものを作り出すのが問題11.7である。
さて、定理11.1により、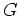 の表現論のかなりの部分は全行列環
の表現を調べることに帰着される。実は全行列環の表現は限られたものしかない。
の表現論のかなりの部分は全行列環
の表現を調べることに帰着される。実は全行列環の表現は限られたものしかない。
定理 11.3
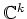
は自然なやり方で
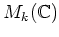
-加群と見ることができる。
これをここでは
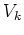
と書くと、
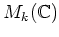
の任意の有限次元表現は
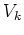
の有限個の直和と(
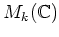
加群として)
同型である。 とくに、
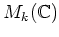
の有限次元既約表現は必ず
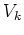
と同型である。
問題 11.1
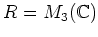
のとき、補題
11.3 の条件(1),(2),(3)を満たす
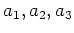
を
見つけ出し、その
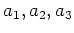
にたいして
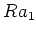
,
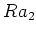
,
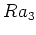
に入るための条件をできるだけ具体的に書け。
問題 11.2
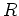
の左
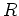
-部分加群(つまり、
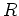
の左イデアル)
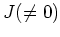
が
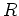
-加群として既約ならば、
ある
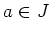
があって、
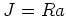
が成り立つことを示せ。
(ヒント:
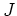
の任意の元
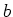
に対して、
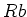
も
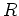
の左イデアルである。 )
問題 11.3
補題
11.3 の(1),(2) が成り立つような
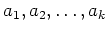
に対して、
同補題の(3)が成り立つことを示せ。
(ヒント:
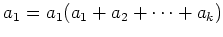
の右辺を展開し、両辺の分解(1)に
関する成分を比較せよ。
問題 11.4
補題
11.3の仮定のもとで
どの
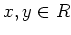
にたいしても、
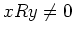
であること、
すなわち、ある
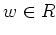
があって
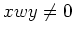
であることを示しなさい。
(ヒント:
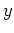
を一つ固定する毎に、
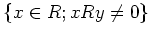
は
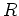
の両側
イデアルになる。)
問題 11.5
体
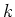
上有限次元の環
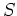
が、非自明な左イデアルをもたないと仮定する。
このとき、
が成り立つことを示しなさい。
(ヒント:
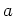
が 0 でないとすると、
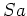
は
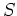
の左イデアルで、0 ではないから、
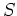
にならざるを得ない。ここから
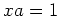
なる
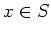
の存在を導く。)
問題 11.6
補題
11.5を証明せよ。(ヒント:任意の
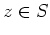
にたいして、
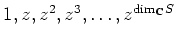
は一次独立たり得ないため、
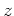
は
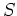
上ある方程式をみたす。そのような方程式のうち
次数が最小のもの(
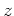
の最小多項式) を
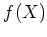
とすると、代数学の基本定理により
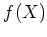
は
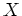
の一次式の積に分解する。つまり、
なる
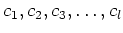
が存在する。
あとは前問をもちいる。)



: この文書について...
2003/7/5
![]() の表現を全て求めるための決定打が、次の定理だ。
の表現を全て求めるための決定打が、次の定理だ。
![]() を中心元による固有分解することによって、上の定理は次の
命題に帰着される。
を中心元による固有分解することによって、上の定理は次の
命題に帰着される。
![]() に
該当するものを見つけ出してくるかというところにある。
に
該当するものを見つけ出してくるかというところにある。
![]() に対して、
に対して、
![]() というのが
上の補題の代表的な例である。
というのが
上の補題の代表的な例である。
![]() にあたるものを作り出す。
にあたるものを作り出す。
![]() の表現論のかなりの部分は全行列環
の表現を調べることに帰着される。実は全行列環の表現は限られたものしかない。
の表現論のかなりの部分は全行列環
の表現を調べることに帰着される。実は全行列環の表現は限られたものしかない。