![]()
前回の流れから行くと、行列 ![]() をまず弱固有空間ごとに分けて考えて、
それぞれの部分で
をまず弱固有空間ごとに分けて考えて、
それぞれの部分で ![]() の標準型を考えるのが自然であるのだが、
若干見方をかえて加群の理論から話を進めよう。
の標準型を考えるのが自然であるのだが、
若干見方をかえて加群の理論から話を進めよう。
![]() 次正方行列
次正方行列
![]() が与えられているとする。
が与えられているとする。![]() は
は
さて、![]() の成分を多項式に拡張して、
の成分を多項式に拡張して、
![% latex2html id marker 839
$\displaystyle F_0={\mathbb{C}}[X]^n
=\left\{
\begi...
..._n(X)
\end{pmatrix} ; a_i (X)\in {\mathbb{C}}[X] \quad(i=1,2,\dots,n)
\right\}
$](img11.png)
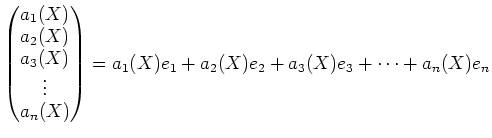
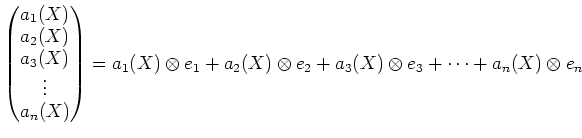
テンソル記号をドットに置き換える操作を ![]() と書こう。
すなわち、
と書こう。
すなわち、
![]() を
を
![]() は線型写像で、全射であることはすぐに分かる。
は線型写像で、全射であることはすぐに分かる。
![]() の核は、次のような線型写像の像と一致する。
の核は、次のような線型写像の像と一致する。
![]() を
を ![]() と
と ![]() の基底を取り換えることによって、できるだけ
やさしい表示にすること、これがポイントである。
実は、
の基底を取り換えることによって、できるだけ
やさしい表示にすること、これがポイントである。
実は、 ![]() のような特殊な元に限らず、そのようなやさしい表示がある。
のような特殊な元に限らず、そのようなやさしい表示がある。
すなわち、
![]() ではユークリッド除法(余りを許した割り算)ができることから、
「掃き出し法」が使えて、次のような命題が成り立つ。
ではユークリッド除法(余りを許した割り算)ができることから、
「掃き出し法」が使えて、次のような命題が成り立つ。
(ただし
上の
![]() は
は ![]() の単因子と呼ばれる。
の単因子と呼ばれる。
上の ![]() はそれぞれ
次のような「基本変形」を具体的に表現するような行列の積である。
はそれぞれ
次のような「基本変形」を具体的に表現するような行列の積である。
この続きは次回にまわす。