


: この文書について...
代数学II 要約 No.11
今日のテーマ:

補題 11.1
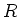
は環で、ある素数
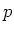
があって、
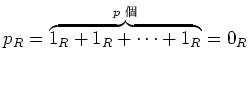
が
成り立っているとする。
このとき、
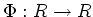
を
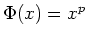
で定義すれば、
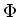
は
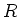
からそれ自身への準同型(自己準同型)を与える。
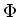 を
を 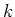 回繰り返した写像
回繰り返した写像 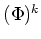 は
で与えられることにも注意しておく。
は
で与えられることにも注意しておく。
定義 11.1
素数
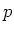
のベキ
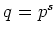
にたいして、
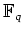
の拡大体
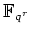
の自己同型
を
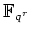
の
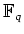
上のフロベニウス自己同型と呼ぶ。
補題 11.3
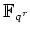
の
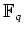
上の自己同型
(
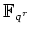
から
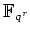
への自己同型写像で
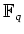
に制限すると恒等写像になるもの)の全体は、
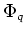
によって生成される位数
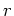
の巡回群である。
次の補題は補題11.2の(1)の拡張にあたる。
補題 11.4
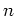
変数の多項式
![% latex2html id marker 1240
$ f_1,f_2,\dots,f_m \in {\mathbb{F}}_q[X_1,X_2,\dots,X_n]$](img30.png)
の
決める方程式系
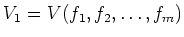
に対して、
「フロベニウス写像」
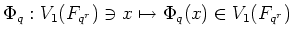
を次のようにして定義できる。
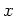
が
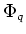
の不動点 (
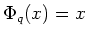
)であることと、
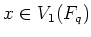
であることとは同値である。
本講義では触れないが、
上の補題は合同ゼータ関数の性質を調べる最初のヒントになる。
1変数方程式のゼータ関数を決定しておこう。
まず既約性についての簡単な補題から
命題 11.1
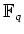
上の既約な1変数多項式
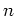
次多項式
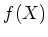
に対して、
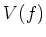
の合同ゼータ関数は
で与えられる。
今回の話をもちいると、次の2問はかなり解きやすくなる。
問題 8.1 次のような(1)-(3)の例を((4)が解きやすいように)作り,(4)を 求
めなさい。
(1) 素数 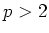
(2) 正の整数 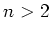
(3)
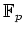 上の相異なる
上の相異なる 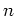 次既約多項式
次既約多項式
![$ f,g\in{\mathbb{F}}_p[X]$](img54.png)
(4)
![$ {\mathbb{F}}_p[X]/f(X){\mathbb{F}}_p[X]$](img55.png) での
での 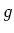 の一次式への
分解
の一次式への
分解
問題 9.1 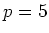 とする。
とする。
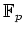 上のモニックな4次既約多項
式
上のモニックな4次既約多項
式 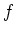 の例を挙げ、
の例を挙げ、 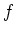 の一つの根を
の一つの根を 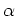 とした時、
とした時、 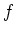 の他
の根を
の他
の根を 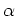 であらわしなさい。 (つまり、
であらわしなさい。 (つまり、 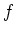 を
を
![$ {\mathbb{F}}_p[\alpha]$](img58.png) 上で一次式の積に分解しなさい。)
上で一次式の積に分解しなさい。)
問題 11.1
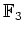
上の多項式
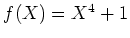
に対して、
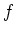 を
を
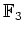 上の既約な多項式の積に分解しなさい。
上の既約な多項式の積に分解しなさい。
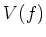 の合同ゼータ関数
の合同ゼータ関数 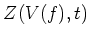 を求めよ。
を求めよ。
(ヒント:
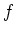
は
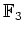
上
既約ではないので、命題
11.1は
そのままでは使えない。)
問題 11.2
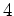
で割ると
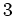
余るような素数
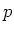
に対しては、
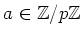
を
どのように選んでも、
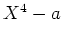
は
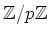
上既約にならないことを示しなさい。
(ヒント:任意の素数 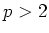 と
と
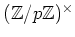 の生成元
の生成元 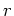 とに対して、
とに対して、
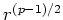 は
は
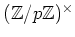 の位数
の位数 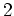 の元である。(なぜか?))
の元である。(なぜか?))
問題 11.4
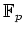
の元
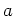
で、どんな
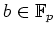
をとってきても
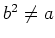
を満たすものが与えられたとする。
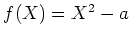
とし、
![$ R={\mathbb{F}}_p[X]/f(X){\mathbb{F}}_p[X]$](img77.png)
を
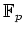
上の
2次元ベクトル空間と見たとき、
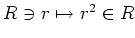
を表示するような
2次行列
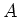
をもとめ、
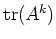
を計算しなさい。
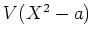
の合同ゼータ関数とこの結果の関係について、わかることを
(思い付く限り)述べよ。
(
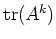 は
は
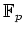 の元であるから、「個数」という量(
の元であるから、「個数」という量(
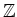 の元)
と比べると少し情報量が落ちる。
この問題で、
の元)
と比べると少し情報量が落ちる。
この問題で、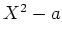 を任意の既約多項式に置き換えても同様のことが
できるのだが、それは少し難しすぎるので、ここでは問題としては課さない。)
を任意の既約多項式に置き換えても同様のことが
できるのだが、それは少し難しすぎるので、ここでは問題としては課さない。)



: この文書について...
2002年7月2日
![]()
 が
成り立っているとする。
このとき、
が
成り立っているとする。
このとき、
![]()
![]()
![]() 上の相異なる
上の相異なる ![]() 次既約多項式
次既約多項式
![]()
![]() での
での ![]() の一次式への
分解
の一次式への
分解
![]() とする。
とする。
![]() 上のモニックな4次既約多項
式
上のモニックな4次既約多項
式 ![]() の例を挙げ、
の例を挙げ、 ![]() の一つの根を
の一つの根を ![]() とした時、
とした時、 ![]() の他
の根を
の他
の根を ![]() であらわしなさい。 (つまり、
であらわしなさい。 (つまり、 ![]() を
を
![]() 上で一次式の積に分解しなさい。)
上で一次式の積に分解しなさい。)