今日のテーマ:
![]()
先週、次の定理が残ってしまっていた。
次の系は有限体(等いろいろな体)を作る際の基本である。
![]() が有限体 (例えば、
が有限体 (例えば、
![]() )
ならば上の補題のようにして作られた体は必然的に有限体になる。
)
ならば上の補題のようにして作られた体は必然的に有限体になる。
![]() での
での ![]() のクラスを
のクラスを ![]() と書くと、
と書くと、![]() は
は ![]() に
に ![]() という一つの元を付け加えた体になっている。このような体を
という一つの元を付け加えた体になっている。このような体を ![]() の単純拡大体
と呼ぶ。
の単純拡大体
と呼ぶ。
![]() の既約元を発見する方法についてはあとあと述べる予定であるが、
取りあえず次のことぐらいはとりあえず知っておくとよいだろう。
の既約元を発見する方法についてはあとあと述べる予定であるが、
取りあえず次のことぐらいはとりあえず知っておくとよいだろう。
この段階で, 有限体の演算の実際について知っておくのも悪くはなかろう。 加、減、乗算についてはそんなに難しくはないと思われるので、 ここでは 0以外の元の逆元の計算法について簡単に触れておく。 要はユークリッドの互除法であって、代数学I ですでに目にしているはずである。 まずユークリッドの互除法の簡単な復習から。
(解答) まず次のような計算を行なう
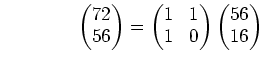 |
||||||||||||
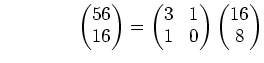 |
||||||||||||
| 0 | 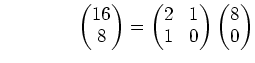 |
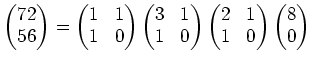
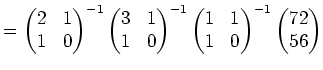 |
||
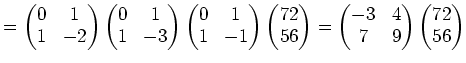 |
(答え)
![]() .
.
(解答)
上の例題4.1の要領で
![]() なる
なる
![]() を求めることにより、
を求めることにより、