

: 前小節の補遺
: その1:基本列ベクトル
: を実ベクトル空間とみる。
この小節の内容は線型代数から逸脱しているが、ついでだから付け加えておく。
代数の講義を受けてから振り返ってみるとよいだろう。
環 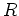 と、その元
と、その元
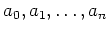 が与えられているとき、
が与えられているとき、
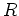 に元
に元 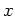 を付け加えた環
を付け加えた環 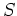 を作り、
を作り、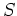 のなかで
のなかで 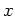 が
が
の根になるようにしたい、
つまり、
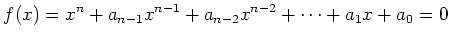 |
(※) |
が成り立つようにしたいということがたまにある。
(例えば、
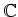 は
は
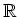 に
に 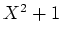 の根を付け加えたものである。)
の根を付け加えたものである。)
もしそのような 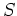 が仮にあったとすれば、
が仮にあったとすれば、
であることがわかる。というのも、
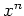 は関係式 (※)により
は関係式 (※)により 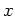 の
の 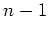 次以下の
多項式で表現しなおすことができる
し、
次以下の
多項式で表現しなおすことができる
し、
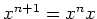 も
いったん
も
いったん 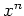 を (※) で
を (※) で 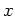 の
の 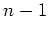 次以下の多項式に置き換え、
その後この式を展開して出て来た
次以下の多項式に置き換え、
その後この式を展開して出て来た 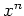 をもう一度 (※)を使って
をもう一度 (※)を使って 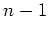 次以下に
置き換えることができる。
次以下に
置き換えることができる。
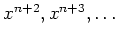 も同様であるからである。
も同様であるからである。
となると、やはり
に 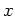 倍がどのように作用するかが問題になる。
前小節と全く同様な考察により、それは
倍がどのように作用するかが問題になる。
前小節と全く同様な考察により、それは 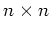 -行列
という行列と対応することがわかる。
-行列
という行列と対応することがわかる。
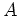 は
は 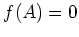 を満足することにも
注意しておこう。
このように、行列により、
を満足することにも
注意しておこう。
このように、行列により、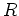 上の方程式
上の方程式 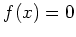 を満足する
ような
を満足する
ような 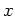 を具体的に構成できるわけである。
を具体的に構成できるわけである。
平成15年1月30日
![]() と、その元
と、その元
![]() が与えられているとき、
が与えられているとき、
![]() に元
に元 ![]() を付け加えた環
を付け加えた環 ![]() を作り、
を作り、![]() のなかで
のなかで ![]() が
が
![]() が仮にあったとすれば、
が仮にあったとすれば、

![]() は
は ![]() を満足することにも
注意しておこう。
このように、行列により、
を満足することにも
注意しておこう。
このように、行列により、![]() 上の方程式
上の方程式 ![]() を満足する
ような
を満足する
ような ![]() を具体的に構成できるわけである。
を具体的に構成できるわけである。