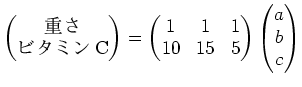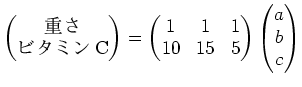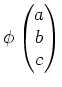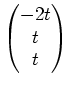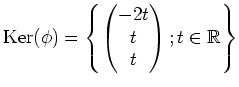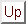

: 準同型定理
: 線型写像
: 栄養をとろう
ダジャレ空間の元に対して、ビタミンCと、トータルの重さのみに着目してみよう。
右辺のことを
と書くことにしよう。
いま、重さを 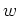 (
(
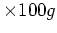 )で、 ビタミンC が
)で、 ビタミンC が 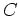 (
(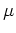 g)
になるようにしたいとするとどうだろう。
g)
になるようにしたいとするとどうだろう。
幾つかの答えがあることがわかる。
答えが一つに絞られないのは、3種類の野菜で 2つの量
(重さとビタミンC)のみしかコントロールしないわけだから
当然であるともいえる。
とくに、
は 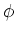 で写してやって 0 である。
ビタミンC と重量の点だけから言うと、「ダイコン 200g 」と
「ジャガイモ 100g + レタス 100g 」とは全く等価であるわけだ
5。
一般に、幾つかの野菜をとったとして、そのトータルの成分、重量、価格
をコントロールするときに、上のように全然別の組合せが(考えている成分等
のみに関して言えば)等価になることがある。
これが線型写像の核の考え方である。
で写してやって 0 である。
ビタミンC と重量の点だけから言うと、「ダイコン 200g 」と
「ジャガイモ 100g + レタス 100g 」とは全く等価であるわけだ
5。
一般に、幾つかの野菜をとったとして、そのトータルの成分、重量、価格
をコントロールするときに、上のように全然別の組合せが(考えている成分等
のみに関して言えば)等価になることがある。
これが線型写像の核の考え方である。
上の場合で言うと、
ということになる。
平成15年1月30日