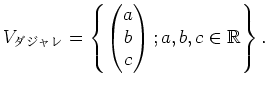
次のような「ダジャレ空間」を考える。
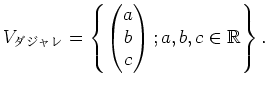
| ダイコン | ジャガイモ | レタス | |
| ビタミン A | 0 | 0 | 300 |
| ビタミン C | 10 | 15 | 5 |
| カリウム | 250 | 350 | 200 |
| ナトリウム | 20 | 1 | 2 |
| 葉酸 | 35 | 25 | 75 |
ダイコンを ![]() , ジャガイモを
, ジャガイモを ![]() , レタスを
, レタスを ![]() (単位は
(単位は ![]() )
だけ食べたとして、そのとき摂取した栄養はと言えば、上の表から
)
だけ食べたとして、そのとき摂取した栄養はと言えば、上の表から
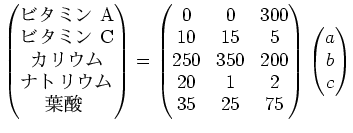
このようにして得られる写像
今は適当な栄養素だけを抜きだして計算したが、 栄養素の数を減らしても、増やしても、同様の話ができるし、 ダジャレ空間以外で同じような話を考えることもできる。
ほかにもこのような計算はあちこちで見られる。
「マトリックス(行列)はどこにでもある」
といわれるゆえんである。