一次独立(線型独立)性

またもや初等コーヒベクトル空間について考えよう。「初等」だから コーヒ、水、砂糖、ミルクの4種類(正確には、4成分)の 量のみを問題にすることは、前に述べた通りである。

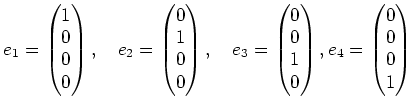
負の成分について悩む可能性を減らすために、次の状況を考えることにする。

(*) 「究極の」初等コーヒレシピをつくろう。 既にコーヒーのレシピの大枠は決まっていて、あとはコーヒ,水,砂糖,ミルクの量を ミリグラム単位で増減してぴったりのやつを作ればよい。

線型代数の手法は、しばしばこのような「微小の増減」を問題にする時に 有効になる。 (厳密に言えば、最初のコーヒ等の量を上回る値を減らすことなどには意味がない。 これはこの比喩の限界である。) 多変数関数の微分なども、この伝で説明できるのであるが、ここではそれについては これ以上は触れない。

さて、レシピを作る時に、分かりやすいのは、

1. 粉コーヒ
2. 純水
3. 粉砂糖
4. 粉ミルク

の量を混ぜ込んだり、減らしたりすることで、 これは基本ベクトル

$$e_1= \begin{pmatrix} 1 \\ 0 \\ 0\\ ... ...\\ 0 \\ \end{pmatrix}, e_4= \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}$$

の4つを適当に定数倍して足したり引いたりしてやることに相当することは、 あなたにもお分かりになるだろう。

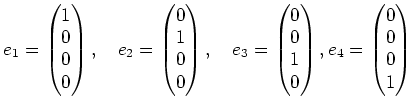
しかし、粉ミルクや砂糖ではなくて、牛乳や液体砂糖(これらは水分を含む)を 使っているかも知れない。この場合、牛乳を足すと水分も増える(結果として コーヒは少し薄くなる。)ということに注意を払わなければならない。 そう。牛乳を加えるということは、例えば

$$e_{\text{牛乳}}= \begin{pmatrix} 0 \\ 10 \\ 0 \\ 1 \end{pmatrix}$$

という牛乳ベクトルの何倍かを加えることに相当するわけだ。 液体砂糖についても同様のことが言えて、これはたとえば

$$e_{\text{液体砂糖}}= \begin{pmatrix} 0 \\ 5 \\ 0 \\ 1 \end{pmatrix}$$

という液体砂糖ベクトルの何倍かを加えることを考えることになる。

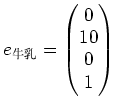
さて、粉コーヒ,水,砂糖、粉ミルク,牛乳,液体砂糖とでてきた。 それ以外にもコーヒと粉ミルクを混ぜた「インスタントミルクコーヒの粉」

$$e_{\text{IMC}}= \begin{pmatrix} 3 \\ 0 \\ 0 \\ 1 \end{pmatrix}$$

とか、同種のもので砂糖入のものとか、いろいろバリエーションを考えられる。

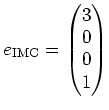
これらのレシピからの量を増やしたり減らしたりして 好みの味を作りたいわけだが、今は4成分の量のみを問題にしているので、 言うまでもなくこれらの全てを増減させなくてもよい。

水分が足らないと思ったら、牛乳を足して、そのぶん粉ミルクを減らす (現実的には、粉ミルクの代わりに牛乳を使う、ということが多いだろうが) という方法も使えるわけだ。

ひとことで言うと、4つの成分を調整するのに、そんなにたくさんの材料を 増減する必要はない。4つで十分である。その4つは先のベクトルに対応する 4つであってもよいし、それ以外でも良い。ただし、たとえば、

水、粉ミルク、砂糖,牛乳

ではコーヒの量が調整できない。 これは4つと言っても水+粉ミルクで牛乳の代用ができるわけだから、 実質的には材料は3つなわけだ。

同様に、

砂糖、粉ミルク、液体砂糖、牛乳、水

でもダメである。これは5つもあるのにやっぱりコーヒ成分が調節できない。 やっぱり実質的には材料は3つなわけだ。

実質的に何個材料があるか、これに答えるのがベクトルの一次独立、 一次従属(線型独立、線型従属ともいう)の考え方である。