

: 実ベクトル空間でないものの例
: ベクトル空間の定義
: ベクトル空間の定義の勘どころ
正の数 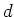 に対して、
は実ベクトル空間である。コーヒベクトル空間はこの例の
に対して、
は実ベクトル空間である。コーヒベクトル空間はこの例の 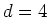 の場合と
見ることができるし、そのほかにもスキヤキベクトル空間、寄せ鍋ベクトル空間、
などなど、この例をもとにした「お伽話」はいくらでも工夫して作れそうである。
各自やってみるとよい。
の場合と
見ることができるし、そのほかにもスキヤキベクトル空間、寄せ鍋ベクトル空間、
などなど、この例をもとにした「お伽話」はいくらでも工夫して作れそうである。
各自やってみるとよい。
実数の全体
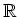 も、通常の和と実数倍によって、実ベクトル空間になっている
ことに注意しておこう。これは (
も、通常の和と実数倍によって、実ベクトル空間になっている
ことに注意しておこう。これは (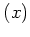 と
と 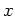 とを同一視することによって、)
上の例の
とを同一視することによって、)
上の例の 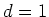 の場合と見ることもできる。
の場合と見ることもできる。
平成15年1月30日
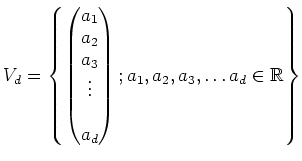
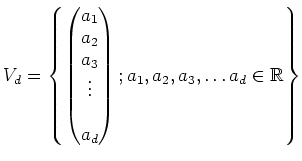
![]() も、通常の和と実数倍によって、実ベクトル空間になっている
ことに注意しておこう。これは (
も、通常の和と実数倍によって、実ベクトル空間になっている
ことに注意しておこう。これは (![]() と
と ![]() とを同一視することによって、)
上の例の
とを同一視することによって、)
上の例の ![]() の場合と見ることもできる。
の場合と見ることもできる。