


Next: About this document ...
代数学特論 II 要約 No.10
今日のテーマ:
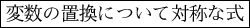 今回は
今回は 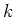 は無限個の元を持つ体とする。
(これには例えば体
は無限個の元を持つ体とする。
(これには例えば体 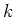 が
が
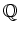 を部分体に含めば十分)
を部分体に含めば十分)
補題 10.1
体
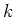
上の
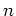
-変数多項式環
![$k[X_1,\dots,X_n]$](img5.png)
の商体(
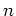
-変数有理関数体)
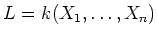
には
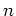
-個の元の対称群
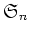
が作用している。
すなわち、任意の
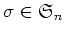
に対して、
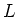
の元
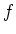
の
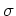
による変換
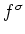
が、
によって定義されて、任意の
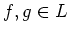
および任意の
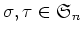
に対して、
- 1.
-
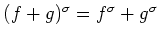
- 2.
-
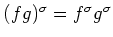
- 3.
-
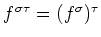
をみたす。
補題にするといかめしいが、要するに変数の置換を行っているだけである。
たとえば、
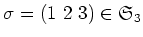 と有理式
と有理式
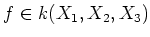 に対して、
に対して、
(もっと具体的には
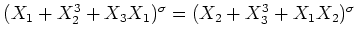 )
等々.
)
等々.
定義 10.1
上の補題の記号の元で、
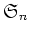
の部分群
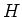
に対して、
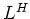
を
で定義する。
例えば
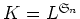 は
は 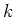 上の
上の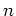 -変数有理式のうち、対称式の
全体を集めたものである。
-変数有理式のうち、対称式の
全体を集めたものである。
定理10.1の証明には次の補題を使えばよい。
上の補題の条件を満たすような 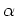 の存在は既に示してあるが、
例えば、
の存在は既に示してあるが、
例えば、
補題 10.3
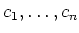
が
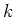
の相異なる元ならば、
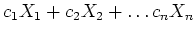
は上の補題の
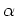
の条件を満たす。
問題 10.1
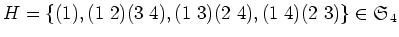
とする。このとき、
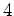
-変数有理関数体
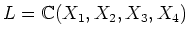
の
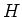
-不変元全体のなす体
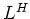
の元を10個挙げなさい。
(どのような元をとるかは自由だが、できるだけ自明でないものを選ぶよう
努力していただきたい。)
2002-01-07
![]() 今回は
今回は ![]() は無限個の元を持つ体とする。
(これには例えば体
は無限個の元を持つ体とする。
(これには例えば体 ![]() が
が
![]() を部分体に含めば十分)
を部分体に含めば十分)![]() と有理式
と有理式
![]() に対して、
に対して、
![]() は
は ![]() 上の
上の![]() -変数有理式のうち、対称式の
全体を集めたものである。
-変数有理式のうち、対称式の
全体を集めたものである。
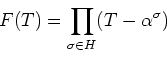
![]() の存在は既に示してあるが、
例えば、
の存在は既に示してあるが、
例えば、