


Next: About this document ...
代数学 II 要約 No.5
今日のテーマ:

補題 5.1
- 1.
-
![$k[X_1,\dots,X_n]$](img2.png) の各元は
の各元は 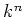 上の
上の 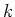 -値関数と見ることができる。
-値関数と見ることができる。
- 2.
- この対応によって、多項式の足し算、引き算、かけ算は各点での足し算、
引き算、かけ算に対応する。
- 3.
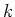 の元の個数が無限個ならば
の元の個数が無限個ならば
![$p\in k[X_1,\dots, X_n]$](img5.png) はその
はその 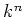 での
値によって完全に決定される。
での
値によって完全に決定される。
定義 5.1
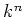
の代数的集合
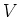
に対して、
![$k[X_1,\dots,X_n]/I(V)$](img10.png)
のことを
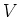
の座標環と呼び、
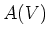
とかく。
補題により 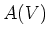 は 「
は 「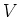 上の
上の 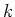 -値関数全体の集合」の
部分集合を与えることがわかる。
-値関数全体の集合」の
部分集合を与えることがわかる。
(補足)
一般に、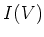 以外の
以外の
![$R=k[X_1,\dots,X_n]$](img13.png) のイデアル
のイデアル 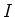 に対しても、
に対しても、
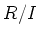 が「座標環」とみなせるような幾何学的対象があると便利である。
そのようなもののうち一番ポピュラーなものはアファインスキーム
が「座標環」とみなせるような幾何学的対象があると便利である。
そのようなもののうち一番ポピュラーなものはアファインスキーム
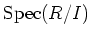 とよばれるもので、抽象的な代数幾何学では中心的な役割を果たす。
とよばれるもので、抽象的な代数幾何学では中心的な役割を果たす。
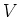 の座標環は
の座標環は 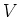 の情報をかなり握っている。今回はそのなかの一つだけを
述べよう。
の情報をかなり握っている。今回はそのなかの一つだけを
述べよう。
補題 5.3
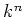
の代数的集合
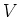
が与えられているとする。
もし、
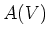
が
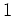
以外の巾等元
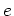
(すなわち、
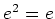
となる元)
をもてば、
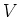
は互いに交わらない空でない代数的集合
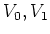
の
和集合になる。
具体的には、
Zariski 位相の定義を思い起こせば、上の補題は次のように言うこともできる。
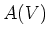 が
が 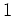 以外の巾等元を持てば、
以外の巾等元を持てば、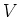 は(
は(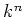 の Zariski 位相からの
誘導位相について)連結でない。
の Zariski 位相からの
誘導位相について)連結でない。
(実際にはこの命題の対偶の方が意味がとりやすいだろう。)
レポート問題は5.1または5.2を選択すること。
両方選択してもよいが、評価されるのはどちらかよい方のみである。
問題 5.1
次の各々の環の巾等元(
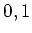
を含む)を指定する数だけ求めなさい。
(答えは
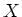
ないし
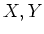
の多項式で書き表し、できるだけ次数の低いものを
求めるように努力すること。
また、各々の巾等元
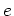
について、ちゃんと
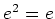
を満たすことを
示しておくこと。
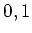
については省略してもよい。)
- 1.
-
![$\mbox{${\Bbb R}$ }[X]/\langle X^3-X\rangle_{\text{ideal}}$](img26.png) (
(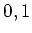 を含めて8つ)
を含めて8つ)
- 2.
-
![$\mbox{${\Bbb R}$ }[X,Y]/\langle X^2Y-X\rangle_{\text{ideal}}$](img27.png) (
(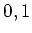 を含めて4つ)
を含めて4つ)
(注意)
上の問題では、諸君の注意を促すために
という記号を用いたが、たびたび言うようにこれは
と書かれることの方が多い。
問題 5.2
- 1.
-
![${\Bbb C}[X,Y,Z]/(XZ-1,X-Y,X+Y)$](img30.png) の巾等元で、
の巾等元で、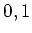 以外のものを二つあげよ。
以外のものを二つあげよ。
- 2.
- 一般には補題5.3の逆は正しくない。
その例をあげよ。
Yoshifumi Tsuchimoto
2001-05-14
![]()
![]() は 「
は 「![]() 上の
上の ![]() -値関数全体の集合」の
部分集合を与えることがわかる。
-値関数全体の集合」の
部分集合を与えることがわかる。
![]() 以外の
以外の
![]() のイデアル
のイデアル ![]() に対しても、
に対しても、
![]() が「座標環」とみなせるような幾何学的対象があると便利である。
そのようなもののうち一番ポピュラーなものはアファインスキーム
が「座標環」とみなせるような幾何学的対象があると便利である。
そのようなもののうち一番ポピュラーなものはアファインスキーム
![]() とよばれるもので、抽象的な代数幾何学では中心的な役割を果たす。
とよばれるもので、抽象的な代数幾何学では中心的な役割を果たす。
![]() の座標環は
の座標環は ![]() の情報をかなり握っている。今回はそのなかの一つだけを
述べよう。
の情報をかなり握っている。今回はそのなかの一つだけを
述べよう。
![]() が
が ![]() 以外の巾等元を持てば、
以外の巾等元を持てば、![]() は(
は(![]() の Zariski 位相からの
誘導位相について)連結でない。
の Zariski 位相からの
誘導位相について)連結でない。