


Next: About this document ...
代数学特論 I 要約 No.1

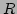 が 体
が 体 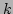 上の 1変数多項式環
上の 1変数多項式環 ![$k[X]$](img4.png) のときと
整数環
のときと
整数環 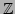 の時のそれぞれについて、
の時のそれぞれについて、
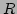 のイデアル
のイデアル 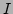 と、
と、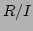 の様子を、とくに
の様子を、とくに 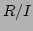 が整域でない時を
中心に調べる。
が整域でない時を
中心に調べる。
今日のテーマ:

定義 1
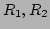
は単位元をもつ環であるとする。
このとき、
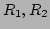
の環としての直積
とは、デカルト積集合
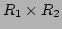
の上に、
次のような演算を定義した物である。
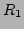
と
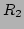
の環としての直積を、普通
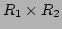
と書く。
次の二つの補題を用いると、上の定理の適用例がたくさん作れる。
補題 2
単位元をもつ可換環
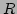
の元
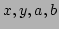
が、関係式
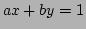
を満たせば、
- 1.
-
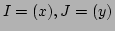 は定理1 の仮定を満たす。
は定理1 の仮定を満たす。
- 2.
-
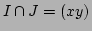 である。
である。
補題 3
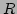
が PID で、 その二つの元
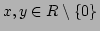
が共通の素因子をもたなければ、
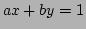
となる
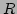
の元
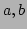
が存在する。
環の直積分解においては、二つの基本的な元が重要な役割を果たす。
上の補題により、環を直積分解したいときには、
 を満たす
元
を満たす
元 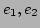 を探せばいいことがわかる。
を探せばいいことがわかる。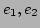 のことを
(直積分解に対応する)射影と呼ぶ。
のことを
(直積分解に対応する)射影と呼ぶ。
※三つの環
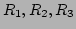 の直積も二つの場合と同様に定義される。
環
の直積も二つの場合と同様に定義される。
環
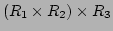 は
は
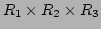 と
同型である。4つ以上でも同様。
と
同型である。4つ以上でも同様。
Yoshifumi Tsuchimoto
2000-10-21
![]()
![]() が 体
が 体 ![]() 上の 1変数多項式環
上の 1変数多項式環 ![]() のときと
整数環
のときと
整数環 ![]() の時のそれぞれについて、
の時のそれぞれについて、
![]() のイデアル
のイデアル ![]() と、
と、![]() の様子を、とくに
の様子を、とくに ![]() が整域でない時を
中心に調べる。
が整域でない時を
中心に調べる。
![]()
![]() の直積も二つの場合と同様に定義される。
環
の直積も二つの場合と同様に定義される。
環
![]() は
は
![]() と
同型である。4つ以上でも同様。
と
同型である。4つ以上でも同様。