$x^x$ の $x=-1/2$ のときの補遺

本文では読者の混乱を避けるために書きませんでしたが、 Web 版で述べているように、お茶会では

$x=-1/2$ のときの $x^x$ について、

$$(-1/2)^{-1/2}=(-2)^{1/2}=(-2)^{2/4}=((-2)^2)^{1/4}= 4^{1/4}=\sqrt{2}$$ (A)

とした解答がありました。これは

$$[e^{x(\operatorname{Log}(x)+2\pi i k)}]_{x=-1/2} =e^{-1/2 (-\operatorname{Log}(2)+(2 k+1)\pi i)} =\pm i\sqrt{2}$$

と矛盾しているように見えます。

他方で

$$((-8)^2)^{1/6}=64^{1/6}=\pm 2 \omega^k \qquad (\omega=\frac{-1+\sqrt{-3}}{ 2}, k=0,1,2)$$

にたいして、「指数法則」 $x^{yz}=(x^y)^z$ を 適用して、

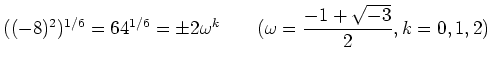
$$((-8)^2)^{1/6}=(-8)^{1/3}=-2 \omega^k \quad (k=0,1,2)$$ (B)

と微妙に違ってくることを気になさっている方もおられます。 とくに、64 の $1/6$ 乗は 2をとりたいところなのに、下段の式にそれが 入っていないことが気になるようです。

ここで解説してしまうとネタバレになってしまうのですが、 どうしても分からなければ御参考になってください。

以下この節では $x$ は 0 ではないとします。

$$x^y=e^{y \log (x)}$$

$$e^{y\operatorname{Log}(x)+2y\pi i k}=e^{y\operatorname{Log}(x)} e^{2y\pi i k} \qquad (k=0,\pm 1,\pm2,\dots)$$

$y$ が整数なら、これはただ一つの値をとって、なんの誤解をも生じ得ません。

$y$ が整数でないときには、 $x^y$ は複数の値をとる、いわゆる多価関数になります。 ($x>0$ のときには $x^y$ を $e^{\operatorname{Log}(x)y}$ で決めると便利なことが多いですが、 それがいつでもベストの答とは限りません。) $x^y$ として上のどれかを 無理に一つを選ぶと、関数の連続性や関数等式が崩れてしまうことが あります。

件の

$$(x^y)^z =x^{yz}$$

はその一例です。

「多価関数」としてみたときはこの等式(「指数法則」)は 条件つきでしか 成り立たないのです。

$x^y$ の $z$ 乗は、上の伝で行くと

$$(x^y)^z=e^{(\operatorname{Log}(x^y)+2\pi m) z} \quad (m=0,\pm 1,\pm 2,\dots)$$

となり、$x^y$ 自身の多価性まで考慮にいれて書くと

$$e^{(\operatorname{Log}(x)+2\pi i n )yz+2\pi i m z} \quad (n,m \in {\mbox{${\mathbb{Z}}$}})$$

で、これは

$$x^{yz}=e^{(\operatorname{Log}(x)+2\pi i n )yz}$$

と比べてとり得る値の幅が違ってしまっているのが分かります。

例えでいうと、 京都から JR で大阪まで行き、そこからさらに私鉄で堺まで行く、 その行き方を時刻表で調べるとします。単に

• 京都から大阪まで
• 大阪から堺まで

の電車の時刻をそれぞれ調べて、それでおしまい、というわけにはいきません。 ちゃんと両者の「接続」というか、うまく時刻がマッチしたものを見つけないと いけないわけです。

多価関数の関数等式でも事情は同じで、二つあるいは三つの多価関数の あいだの等式は、うまくマッチする値を選ばなければならないときがあります。

したがって、多価関数である $x^y$ などに対して 闇雲に指数法則を使って式変形をおこなって 答を得ようとすると間違える、ということになります。(A),(B)は その点でまずい計算をしていることになります。

(もう一つ付け加えておくなら、$x$ が正の値ならば $x^y$ も正のものを とれば常に正しい、(乗り継ぎがうまくいく)と考えるのもまずいわけです。)

こうしてみると、やっぱり多価関数は面倒です。 リーマン面などを駆使して何とか一価関数の世界で済まそうとする気持ちは そんなところからもきています。