Next: About this document ...
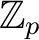 ,
,
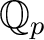 , and the ring of Witt vectors
, and the ring of Witt vectors
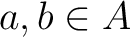 . Assume
. Assume
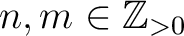 such that
such that
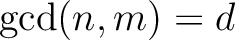 ,
,
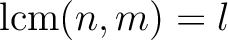 .
Then:
.
Then:
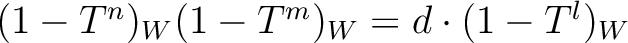
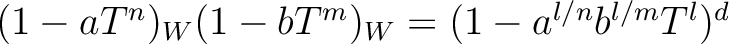
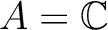 .
unity in
.
unity in
 .
(1)
Let
.
(1)
Let 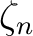 be a primitive root of
unity in
be a primitive root of
unity in
 . Then we have:
. Then we have:
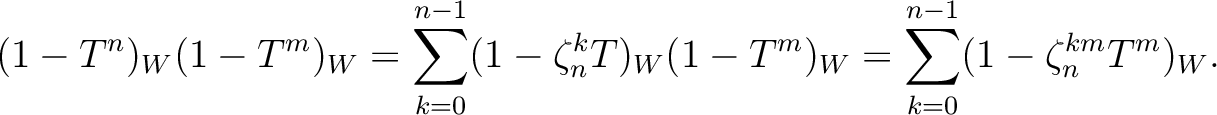 |
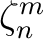 is a primitive
is a primitive 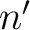 -th root of unity,
we get the desited result.
-th root of unity,
we get the desited result.
(2)
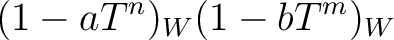 | ||
 |
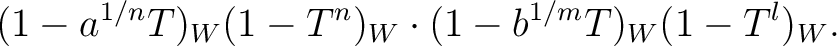 |
By functoriality, we see that the proposition is also valid over the polynomial ring
![$\mathbb{Z}[a,b]$](img20.png) . Then by functoriality we see that
the result is also true for any ring
. Then by functoriality we see that
the result is also true for any ring 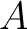 .
.
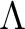
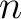 be a positive integer. If
be a positive integer. If 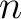 is invertible in
is invertible in 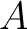 , then
it is also invertible in
, then
it is also invertible in
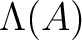 .
.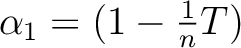 .
Then we have
.
Then we have
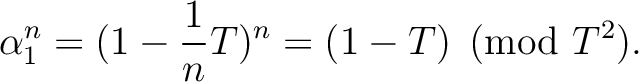
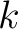 , we have an
polynomial
, we have an
polynomial 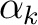 such that
such that
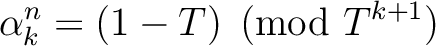
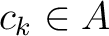 such that
such that
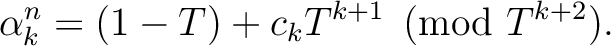
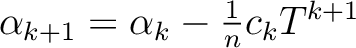 .
.
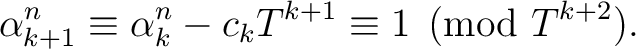
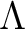
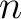 be a positive integer which is invertible in
be a positive integer which is invertible in 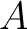 .
The range
.
The range
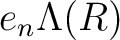 of the idempotent
of the idempotent 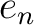 is isomorphic to
is isomorphic to
![$(1+T^n A[[T^n]]) $](img36.png) via
via 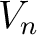
Ring of Witt vectors
Let 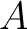 be a ring.
Then
be a ring.
Then
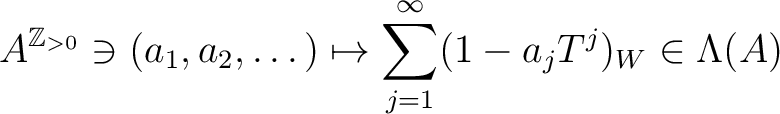
 plays the role of a coordinate of
plays the role of a coordinate of
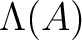 . We call the ring
. We call the ring
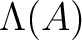 with the coordinate given this way
the ring of Witt vectors.
In this lecture, we do not distinguish too much between
with the coordinate given this way
the ring of Witt vectors.
In this lecture, we do not distinguish too much between 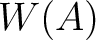 and
and
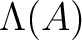 .
.
Verschiebung and Frobenius map.
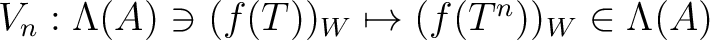
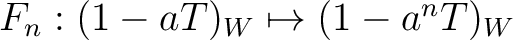
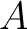 be a ring. Let
be a ring. Let 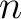 be a positive integer
such that it is invertible in
be a positive integer
such that it is invertible in 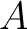 .Then
.Then
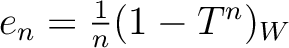 is an idempotent in
is an idempotent in
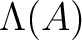 .
.
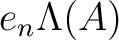 is equal to
the image
is equal to
the image
 of the Verschiebung map. In other words, it
is isomorphic to
of the Verschiebung map. In other words, it
is isomorphic to
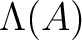 itself via the non-unital isomorphism
itself via the non-unital isomorphism 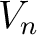 .
.