Next: as a pre-ring Up: , , and the Previous: , , and the
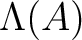 as a
as a 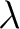 -ring
-ring
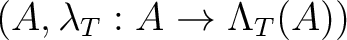 is called a pre-
is called a pre-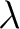 -ring if
-ring if
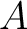 is a commutative ring.
is a commutative ring.
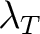 :
:
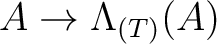 is an additive map.
is an additive map.
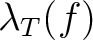 for
for 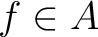 as
as
 .
Then the additivity of
.
Then the additivity of 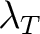 can be expressed as identities of
can be expressed as identities of
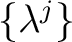 of the following form:
of the following form:
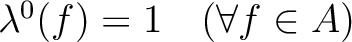 .
.
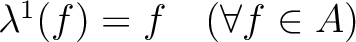 .
.
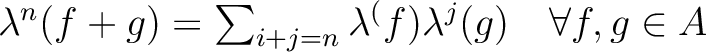 .
.
 is not
a “
is not
a “ -th power of
-th power of 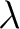 ” in any sence.)
” in any sence.)
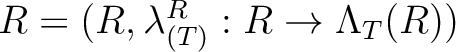 ,
,
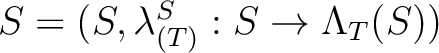 be pre-lambda rings.
Then a
be pre-lambda rings.
Then a 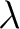 -ring homomorphism from
-ring homomorphism from 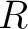 to
to 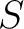 is a ring homomorphism
is a ring homomorphism
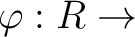 such that the following diagram commutes.
such that the following diagram commutes.
![$\displaystyle \xymatrix
{
R \ar[r]^{\lambda_{(T)}^R} \ar[d]_{\varphi}& \Lambda_...
...[d]^{\Lambda_{(T)}(\varphi)}\\
S \ar[r]_{\lambda_{(T)}^S} &\Lambda_{(T)}(S)
}
$](img30.png)
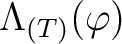 which appears above is defined as follows:
which appears above is defined as follows:

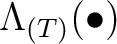 as a functor.)
as a functor.)
![% latex2html id marker 2011
$\displaystyle \Lambda_{(T)}(\varphi)([a])= [\varphi(a)] \qquad( \forall a \in A)
$](img34.png)