Next: Bibliography Up: , , and the Previous: , , and the
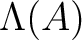
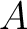 ,
,
![% latex2html id marker 864
$\displaystyle \Lambda(A)=(1+T A[[T]]) \qquad ($](img14.png) as a set
as a set
![$f \in (1+T A[[T]])$](img16.png) , we denote by
, we denote by 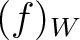 the
corresponding element in
the
corresponding element in
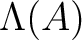 .
.
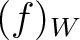 ,
,
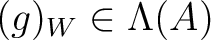 , we define their sum by
, we define their sum by
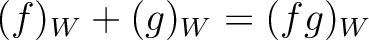
It is easy to see that
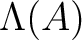 is an additive group.
It also carries the “
is an additive group.
It also carries the “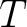 -addic topology” so that
-addic topology” so that
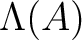 is a
topological additive group.
is a
topological additive group.
The next task is to define multiplicative structure on
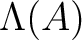 .
To that end, we do something somewhat different to others.
.
To that end, we do something somewhat different to others.
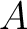 , we define
, we define
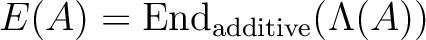 .
It has the usual structure of a ring.
For any
.
It has the usual structure of a ring.
For any  , we define its “Teichmüler” lift
, we define its “Teichmüler” lift ![$[a]$](img23.png) as
as
The basic idea is to define 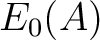 as the subalgebra of
as the subalgebra of 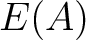 topologically
generated by all the Teichm"uller lifts
topologically
generated by all the Teichm"uller lifts
![$\{[a]; a \in A\}$](img27.png) and identify
and identify 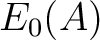 with
with
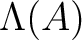 .
To avoid some difficulties doing so, we first do this when
.
To avoid some difficulties doing so, we first do this when 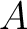 is a very good one:
is a very good one:
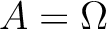 , an algebraically closed field. Then:
, an algebraically closed field. Then:
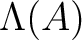 is generated by
is generated by
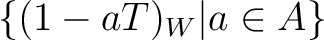 as a topological
additive group.
as a topological
additive group.
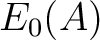 of
of 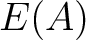 generated by
generated by
![$\{[a]\vert a \in A\}$](img30.png) as a topological ring is equal to
as a topological ring is equal to
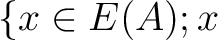 commutes with all Teichmüller lifts
commutes with all Teichmüller lifts .
.
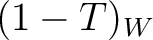 is a generating separating vector of
is a generating separating vector of
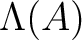 over
over
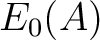 . Thus we have a module isomorphism
. Thus we have a module isomorphism
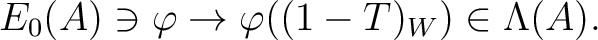
![$[a]$](img23.png) to
to 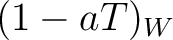 .
.
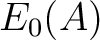 and
and
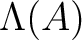 via this
isomorphism and employ a ring structure on
via this
isomorphism and employ a ring structure on
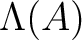 .
.
Here after, for any algebraically closed field 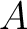 ,
we employ the ring structure of
,
we employ the ring structure of
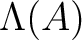 defined as the above proposition.
In this language we have:
defined as the above proposition.
In this language we have:
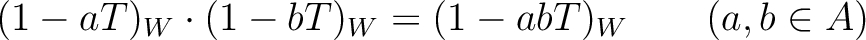
![$f(T)\in 1+TA[[T]]$](img37.png) , we have a formula for
multiplication by degree-1-object
, we have a formula for
multiplication by degree-1-object 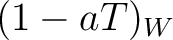 :
:
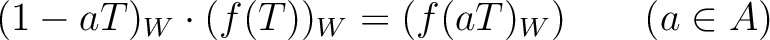
![$g(T)\in 1+TA[T]$](img39.png) with constant term=1.
Indeed, we factorize
with constant term=1.
Indeed, we factorize 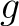 as
as
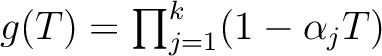 and
and
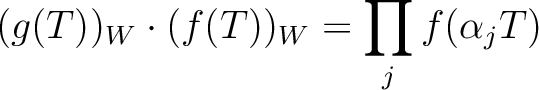
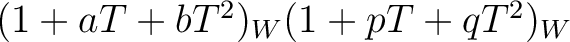 .
Notice that the result of the computation only
needs polynomials with coefficents in
.
Notice that the result of the computation only
needs polynomials with coefficents in
![% latex2html id marker 979
$ \mathbb{Z}[a,b,p,q]$](img44.png) rather than some
extension of the ring.
rather than some
extension of the ring.