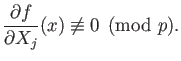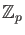 ,
,
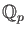 , and the ring of Witt vectors
, and the ring of Witt vectors
No.04:

In this lecture, rings are assumed to be unital, associative and
commutative unless otherwise specified.
DEFINITION 04.1
A (unital commutative) ring
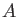
is said to be a
local ring
if it has only one maximal ideal.
PROPOSITION 04.3
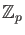 is a local ring. Its maximal ideal is equal to
is a local ring. Its maximal ideal is equal to
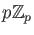 .
.
We may do some “analysis” such as Newton's method to obtain some
solution to algebraic equations.
Newton's method for approximating a solution of algebraic equation.
Let us solve an equation
in
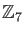 .
We first note that
.
We first note that
hold. So let us put
![$ x_0=3=[0.3]_7$](img10.png) as the first approximation of the solution.
The Newton method tells us that for an approximation
as the first approximation of the solution.
The Newton method tells us that for an approximation 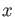 of the equation
of the equation 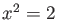 , a number
, a number 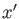 calculated as
calculated as
gives a better approximation.
So
![$ [0.3\dot{1}]_7$](img16.png) is a better approximation of the solution.
In order to make the calculation easier,
let us choose
is a better approximation of the solution.
In order to make the calculation easier,
let us choose
![$ x_1=[0.31]_7$](img17.png) (insted of
(insted of 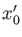 ) as a second approximation.
) as a second approximation.
We choose
![$ x_2=[0.312]_7$](img20.png) as a second approximation.
as a second approximation.
We choose
![$ x_3=[0.31261]_7$](img22.png) as a third approximation.
as a third approximation.
We choose
![$ x_4=[0.312612124]_7$](img24.png) as a third approximation.
as a third approximation.
EXERCISE 04.1
Compute
![$ [0.5]_7/[0.11]_7$](img28.png)
EXERCISE 04.2
Find a solution to
such that
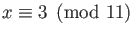
.
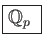
DEFINITION 04.4
We denote by
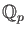
the quotient field of
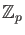
.
LEMMA 04.5
Every non zero element
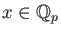 is uniquely expressed as
is uniquely expressed as
We have so far constructed a ring
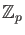 and a field
and a field
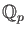 for each prime
for each prime 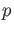 .
.
With
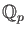 and/or
and/or
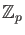 , we may do some “calculus” such as:
, we may do some “calculus” such as:
THEOREM 04.7
[#!Serre2!#, corollary 1 of theorem 1]
Let
![$ f\in \mathbb{Z}_p[X_1,X_2,\dots,X_m], x\in \mathbb{Z}_p^m$](img36.png) ,
,
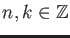 .
Assume that there exists a natural number
.
Assume that there exists a natural number 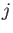 such that
such that
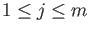 ,
,
Then there exists
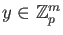 such that
such that
|
(1) |
|
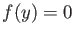 |
|
(2) |
|
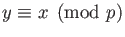 |
See [#!Serre2!#] for details.
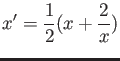
![$\displaystyle x_0'=\frac{1}{2}([0.3]_7+[0.3\dot{2}]_7=[0.3\dot{1}]_7
$](img15.png)
![% latex2html id marker 872
$\displaystyle x_1'
=\frac{1}{2}([0.31]_7+2/[0.31]_7)
=\frac{1}{2}([0.31]_7+[0.3\dot{1}45\dot{2}]_7)\fallingdotseq [0.312]_7
$](img19.png)
![]() as a second approximation.
as a second approximation.
![% latex2html id marker 876
$\displaystyle x_2'
=\frac{1}{2}([0.312]_7+2/[0.3\dot{1}2534066\dot{2}]_7)\fallingdotseq
[0.31261]_7
$](img21.png)
![]() as a third approximation.
as a third approximation.
![% latex2html id marker 880
$\displaystyle x_3'
=
=\frac{1}{2}([0.31261]_7+[0.3126142465066\dots]_7)\fallingdotseq
[0.312612124...]_7
$](img23.png)
![$\displaystyle =\frac{1}{2}([0.312612124]_7+[0.312612124565220422662213135351\dots]_7)$](img26.png)
![]()
![]() and a field
and a field
![]() for each prime
for each prime ![]() .
.
![]() and/or
and/or
![]() , we may do some “calculus” such as:
, we may do some “calculus” such as: