Next: Bibliography Up: , , and the Previous: , , and the
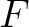 be a finite field (that means,
a field which has only a finite number of elements.)
Then:
be a finite field (that means,
a field which has only a finite number of elements.)
Then:
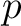 such that
such that 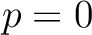 holds in
holds in 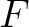 .
.
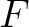 contains
contains
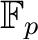 as a subfield.
as a subfield.
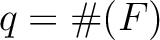 is a power of
is a power of 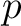 .
.
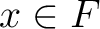 , we have
, we have 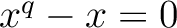 .
.
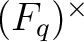 is
a cyclic group of order
is
a cyclic group of order 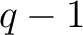 .
.
The next task is to construct such fields. An important tool is the following lemma.
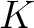 and for any non zero polynomial
and for any non zero polynomial ![$f\in K[X]$](img35.png) ,
there exists a field
,
there exists a field 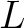 containing
containing 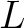 such that
such that
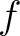 is decomposed into linear factors in
is decomposed into linear factors in 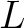 .
.To prove it we use the following lemma.
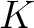 and for any irreducible polynomial
and for any irreducible polynomial ![$f\in K[X]$](img35.png) of
degree
of
degree 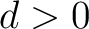 , we have the following.
, we have the following.
![$L=K[X]/(f(X))$](img39.png) is a field.
is a field.
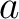 be the class of
be the class of 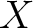 in
in 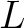 . Then
. Then 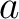 satisfies
satisfies 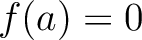 .
.
Then we have the following lemma.
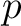 be a prime number. Let
be a prime number. Let 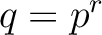 be a power of
be a power of 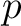 .
Let
.
Let 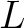 be a field extension of
be a field extension of
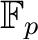 such that
such that 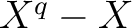 is
decomposed into polynomials of degree
is
decomposed into polynomials of degree 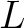 .
Then
.
Then
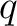
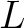 containing
containing
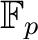 .
.
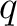 elements.
elements.
Finally we have the following lemma.
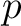 be a prime number. Let
be a prime number. Let 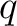 . Then we have the following facts.
. Then we have the following facts.
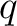 elements.
elements.
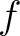 of degree
of degree 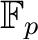 .
.
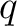 is divisible by the polynomial
is divisible by the polynomial 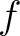 as above.
as above.
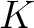 which has exactly
which has exactly 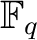 -elements, there exists an element
-elements, there exists an element
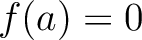 .
.
In conclusion, we obtain:
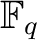 of
of 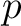 , there exists a field which has exactly
, there exists a field which has exactly 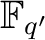 elements.
It is unique up to an isomorphism. (We denote it by
elements.
It is unique up to an isomorphism. (We denote it by
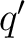 .)
.)
The relation between various
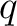 's is described in the following lemma.
's is described in the following lemma.
 to
to
 if and only if
if and only if
 is a power of
is a power of  .
.