Next: 反変、共変ベクトル Up: ベクトル場etcのテンソル積 Previous: ベクトル場etcのテンソル積
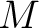 を考える。各点
を考える。各点 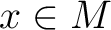 上に仮想的に人間が
いると考えて、それぞれの人がそれぞれ独自に(別々に)数学の問題を考えている
ことを想像するとよい。考える数学の内容は微分積分学、線形代数学など
様々だが、今回は「ベクトル空間、その元、テンソル積、etc」を考えている
図を想像する。
(実際には
上に仮想的に人間が
いると考えて、それぞれの人がそれぞれ独自に(別々に)数学の問題を考えている
ことを想像するとよい。考える数学の内容は微分積分学、線形代数学など
様々だが、今回は「ベクトル空間、その元、テンソル積、etc」を考えている
図を想像する。
(実際には 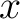 に関する
連続性、可微分性 etc を満たすもののみを考えることが多い。)
に関する
連続性、可微分性 etc を満たすもののみを考えることが多い。)
一般に多様体 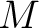 に対して各点
に対して各点 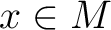 にベクトル空間
にベクトル空間 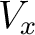 が
与えられているような状況を考える。これをベクトル空間の族とよび、
が
与えられているような状況を考える。これをベクトル空間の族とよび、
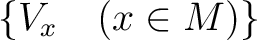 と書くことにする。
(
と書くことにする。
(
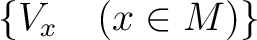 のことを以下では
のことを以下では 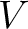 と略すことがある。)
さらに、各
と略すことがある。)
さらに、各 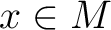 にたいして、
にたいして、
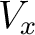 の元
の元 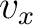 をそれぞれ与えたとき、
をそれぞれ与えたとき、
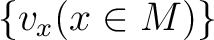 を
を 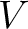 の場
とよぶ。
の場
とよぶ。
族
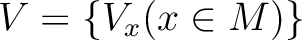 と同じように
と同じように
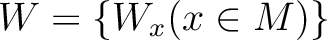 が与えられたとしたとき、新しい族
が与えられたとしたとき、新しい族

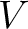 と
と 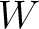 のテンソル積である。
のテンソル積である。