Next: 基底のとり方を変えるとどうなるか Up: ベクトル空間のテンソル積 Previous: ベクトル空間のテンソル積
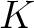 を体とする。不慣れな
を体とする。不慣れな
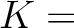
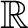 または
または
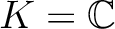 と考えてもよい。
と考えてもよい。
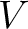 ,
,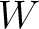 を
を 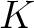 上の有限次元ベクトル空間、
上の有限次元ベクトル空間、
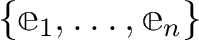 ,
,
 を
それぞれ
を
それぞれ 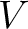 ,
,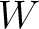 の基底とする。
の基底とする。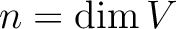 ,
, 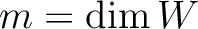 である。
このとき、形式的な元
である。
このとき、形式的な元
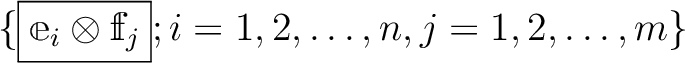
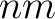 次元の
次元の 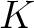 -ベクトル空間を
-ベクトル空間を
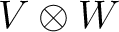 で書き表し、
で書き表し、
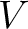 と
と 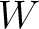 のテンソル積と呼ぶ。
言い換えれば、
のテンソル積と呼ぶ。
言い換えれば、
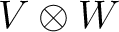 とは形式的な和
とは形式的な和
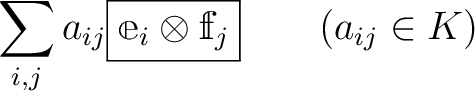
例えば 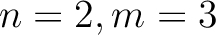 であれば
であれば
 |
|
 |
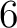 つの元を基底とするベクトル空間が
つの元を基底とするベクトル空間が 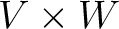 である。
である。
四角で囲うのはいかにも大仰である。しかも
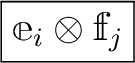 という
記号は要するに
という
記号は要するに 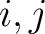 にしか関係しないので
にしか関係しないので
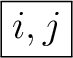 とでも書いておけばそのほうがラクなぐらいだ。
下を参照のこと。
とでも書いておけばそのほうがラクなぐらいだ。
下を参照のこと。
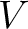 ,
,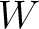 を
を 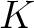 上の有限次元ベクトル空間、
上の有限次元ベクトル空間、
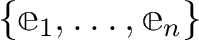 ,
,
 を
それぞれ
を
それぞれ 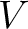 ,
,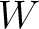 の基底とする。
の基底とする。 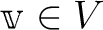 と
と
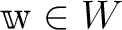 のテンソル積
のテンソル積
 が、次のように定義される
が、次のように定義される
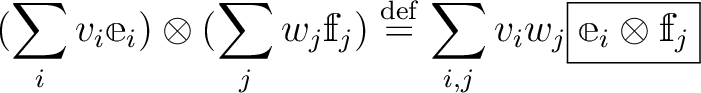
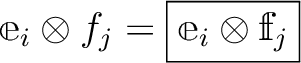
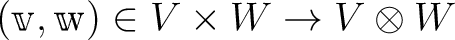 は双線形である。すなわち、
は双線形である。すなわち、
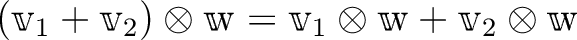
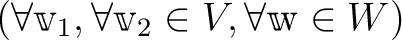 .
.
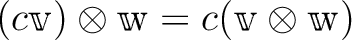
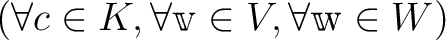 .
.
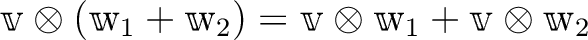
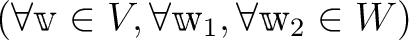 .
.
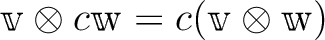
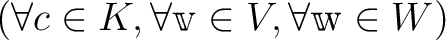 .
.
これで、有限次元のベクトル空間のテンソル積については
(基底さえとれば)おしまいである。