Next: About this document ...
今日のテーマ: (3次元)空間のベクトル
3次元空間の直線の表現法。
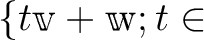
成分で書く方法もある。
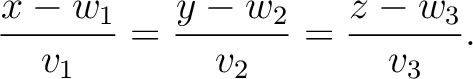
3次元空間の平面の表現法。
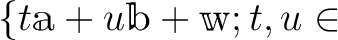
成分で書く方法もある。
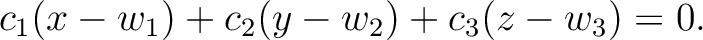
2次元平面での直線の書き方も上に準ずるのであった。
三次元計量ベクトル空間には「外積」という概念もある。 分野によっては大事であるのでここで定義を押さえておこう。
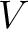 には次のような性質をもつ「外積」が存在する。
には次のような性質をもつ「外積」が存在する。
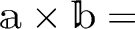
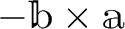
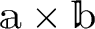 は
は
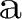 や
や
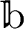 と
直交し、長さは2つのベクトルのつくる平行四辺形の面積
である。
と
直交し、長さは2つのベクトルのつくる平行四辺形の面積
である。
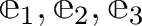 がすでに決まっていて、
がすでに決まっていて、
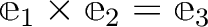 を満たしている、という形で述べるにとどめておく。
を満たしている、という形で述べるにとどめておく。