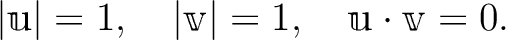Next: About this document ...
今日のテーマ: ベクトル
実数直線も、
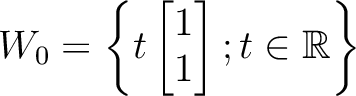 も、「同じ形」をしている。
このような2つを同時に扱うのには、成分を見るのではなく、
和と、スカラー倍という道具のみを用いて記述することが
大事になる。例えば、成分がすべて 0 のベクトル (0 ベクトル) は
も、「同じ形」をしている。
このような2つを同時に扱うのには、成分を見るのではなく、
和と、スカラー倍という道具のみを用いて記述することが
大事になる。例えば、成分がすべて 0 のベクトル (0 ベクトル) は
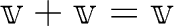 の解と見ることもできる。
の解と見ることもできる。
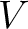 が
が
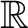 上のベクトル空間であるとは、
つぎの性質を満たしているときにいう。
上のベクトル空間であるとは、
つぎの性質を満たしているときにいう。
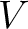 には、和と、
には、和と、
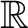 の元による定数倍が定義されている。
の元による定数倍が定義されている。
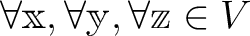 にたいし、
にたいし、
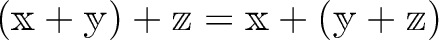 .
.
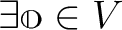 があって、
があって、
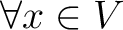 にたいし、
にたいし、
 がなりたつ。
がなりたつ。
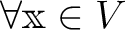 に対して、
に対して、
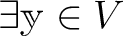 が存在して、
が存在して、
 が成り立つ。
が成り立つ。
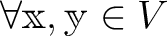 にたいして
にたいして
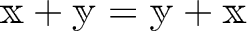 が成り立つ.
が成り立つ.
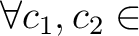
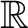
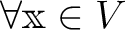
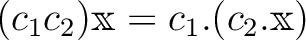 .
.
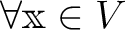
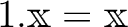 .
.
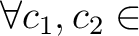
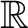
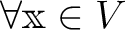
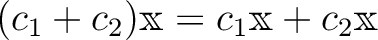
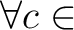
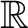
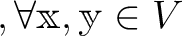
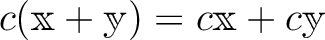 .
.
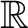 上のベクトル空間
上のベクトル空間 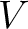 があるとする。
があるとする。
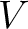 の2つの元
の2つの元
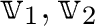 に対して、
内積と呼ばれる実数
に対して、
内積と呼ばれる実数
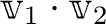 が定義されて、次の性質をみたすとき、
が定義されて、次の性質をみたすとき、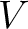 のことを計量ベクトル空間と呼ぶ。
のことを計量ベクトル空間と呼ぶ。
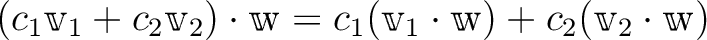 (
(
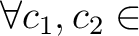
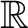
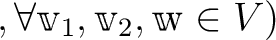
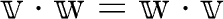 .
(
.
(
 )
)
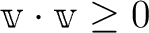 (
(
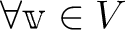 ).
等号は
).
等号は
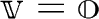 のときのみ。
のときのみ。
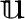 にたいして、
にたいして、
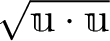 のことを
のことを
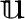 の長さといい、
の長さといい、
 とかく。
とかく。
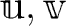 に対して、次が成り立つ。
に対して、次が成り立つ。
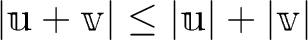 .
.
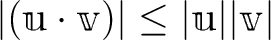 .
とくに
.
とくに
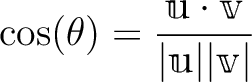 なる
なる 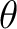 が存在する。これを
が存在する。これを
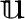 と
と
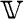 のなす角と呼ぶ。
のなす角と呼ぶ。
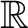 上のベクトル空間が
上のベクトル空間が 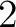 次元であるとは、
次元であるとは、
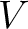 に2つの元
に2つの元
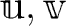 が存在して、次の性質を持つときにいう。
が存在して、次の性質を持つときにいう。
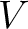 のどの元も
のどの元も
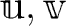 の線型結合で書ける。
の線型結合で書ける。
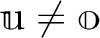 .
.
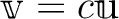 を満たすような実数
を満たすような実数 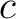 は存在しない。
は存在しない。
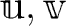 は
は 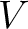 の基底であるという。)
の基底であるという。)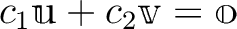 を満たす実数の組
を満たす実数の組
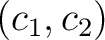 は
は 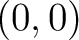 以外には存在しない」というのと同じである。
この条件が満足されるとき、「
以外には存在しない」というのと同じである。
この条件が満足されるとき、「
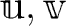 は一次独立である」という。
は一次独立である」という。
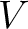 については、次のような基底が存在する。
(正規直交基底)
については、次のような基底が存在する。
(正規直交基底)