Next: About this document ...
今日のテーマ:連立方程式の解法と行基本操作
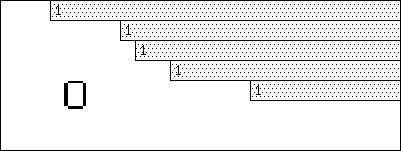
階段行列 ![]() とは、次のような行列である。
とは、次のような行列である。
注意点を 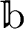 つほど書いておく:
つほど書いておく:
![]() を行基本変形して階段行列
を行基本変形して階段行列 ![]() に直すことができる。
に直すことができる。
![\begin{itembox}[l]{行列の{\bf 行基本操作} とは}
\begin{enumerate}
\ite...
...��する。
\end{enumerate}という操作のことであった。
\end{itembox}](img7.png)
![]() の取り方、直し方はいろいろあるが、
の取り方、直し方はいろいろあるが、
![]() の階数は
の階数は ![]() にしか依らない。
これを
にしか依らない。
これを ![]() の階数と呼び、
の階数と呼び、
![]() で書き表す。
で書き表す。
![]() において、
において、![]() のことを係数行列、
のことを係数行列、
![]() のことを拡大係数行列とよぶ。
のことを拡大係数行列とよぶ。
階数を用いると、連立 ![]() 次方程式の解法は次のように整理できる。
次方程式の解法は次のように整理できる。
 -行列
-行列  -行列
-行列
 (
( 次元列ベクトル)が与えられているとする。
次元列ベクトル)が与えられているとする。
さらに、解を持つときの解空間の次元は
