理工系線形代数学 No.3要約

今日のテーマ:連立方程式の解法と行基本操作

連立一次方程式は行列算で表現できる。例えば、

$$\left \{ \begin{aligned} & x + y= 5 \\ &2 x + 4 y =16 \end{aligned}\right .$$

は

$$\begin{bmatrix} 1 & 1 \\ 2 & 4 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}= \begin{bmatrix} 5 \\ 16 \end{bmatrix}$$

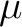
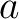
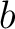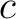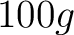と表現できる。 さらに、 $A=\begin{bmatrix} 1 & 1 \\ 2 & 4 \end{bmatrix}$, $\mathbbm x= \begin{bmatrix} x \\ y \end{bmatrix}$, $\mathbbm b = \begin{bmatrix} 5 \\ 16 \end{bmatrix}$ とおけば、 これは更に簡潔に $A \mathbbm x= \mathbbm b$ と表記できる。

更に次のような方程式を考えてみよう。

$$\begin{bmatrix} 1 & 1 \\ 2 & 4 \\ 4 & 5 \end{bmatrix}\begin{bma... ... y \\ \end{bmatrix}= \begin{bmatrix} 5 \\ 16 \\ 23 \end{bmatrix}\tag{あ}$$

$$\begin{bmatrix} 1 & 1 \\ 2 & 4 \\ 4 & 5 \end{bmatrix}\begin{bma... ... y \\ \end{bmatrix}= \begin{bmatrix} 5 \\ 16 \\ 20 \end{bmatrix}\tag{い}$$

$$\begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \end{bmatri... ... y \\ z \end{bmatrix}= \begin{bmatrix} 2 \\ 4 \\ 6 \end{bmatrix}\tag{う}$$

$$\begin{bmatrix} 1 & 1 &0 \\ 0 & 1 & 1 \\ 2 & 4 & 2 \end{bmatrix... ... y \\ z \end{bmatrix}= \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}\tag{え}$$

$$\begin{bmatrix} 1 & 1 &0 \\ 0 & 1 & 1 \\ 2 & 4 & 2 \end{bmatrix... ... y \\ z \end{bmatrix}= \begin{bmatrix} 3 \\ 5 \\ 16 \end{bmatrix}\tag{お}$$

これらの連立方程式は「加減法」によって解けるのであった。 行列でも同じことを行うことができる。行列の行基本操作 とは、

1. ２つの�� を入れ替える。
2. 特定のひとつの�� に、別の�� の定数倍を加える。
3. 特定の一つの�� を定数倍する。

という操作のことを言う。

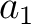
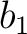
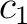
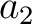
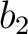
行列は行基本操作を何度も行うことにより、簡単な行列に変形することができる。 このことは、方程式を解くときはもちろん、それ以外の目的でも大変重要である。

ダイコン、ジャガイモ、レタスは それぞれは次のような栄養素をもっている。 ( いずれも100 g あたりの量を 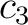$\mu$g 単位で書いてある。 文献を参考にしたので 当てずっぽうというわけでもないが、 かなりいい加減な数字にしてある。)

 

ダイコン	ジャガイモ	レタス
ビタミン A	0	0	300
ビタミン C	10	15	5
カリウム	250	350	200
ナトリウム	20	1	2
葉酸	35	25	75

ダイコンを 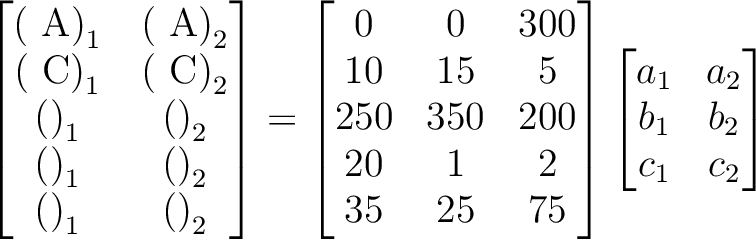$a$, ジャガイモを 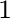$b$, レタスを $c$ (単位は $100g$) だけ食べたとして、そのとき摂取した栄養はと言えば、上の表から

$$\begin{bmatrix} \text{ビタミン A} \\ \text{ビタミン C} \... ... 1 & 2 \\ 35 & 25 & 75 \end{bmatrix}\begin{bmatrix} a\\ b\\ c \end{bmatrix}$$

という行列算で得られるわけだ。 (単に表を行列の記号に直しただけであることに注意。数学者はずぼらだから 罫線なんかは引かないのだ。)

1日目にはダイコンを $a_1$, ジャガイモを $b_1$, レタスを $c_1$ (単位は $100g$) 2日目にはダイコンを $a_2$, ジャガイモを $b_2$, レタスを $c_3$ (単位は $100g$) だけ食べたとして、そのとき摂取した栄養を表に書くと、

$$\begin{bmatrix} \begin{matrix} \text{... ... \end{bmatrix}\begin{bmatrix} a_1 & a_2\\ b_1 & b_2\\ c_1 & c_2 \end{bmatrix}$$

ここで、 (ビタミンA)$_1$ は1日目に摂取したビタミン量...etc である。

今は適当な栄養素だけを抜きだして計算したが、 栄養素の数を減らしても、増やしても、同様の話ができる。

ほかにもこのような計算はあちこちで見られる。