Next: 問題 Up: いくつかの多項式の既約性(例) Previous: いくつかの多項式の既約性(例)
たとえば次のような
![${\mbox{${\mathbb{Z}}$}}[X]$](img6.png) の元の因数分解を考えよう。
の元の因数分解を考えよう。
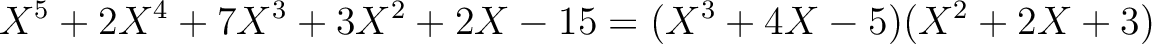
![${\mbox{${\mathbb{Z}}$}}[X]$](img6.png) での
因数分解とも言えるし、多項式の言葉で言えば
での
因数分解とも言えるし、多項式の言葉で言えば
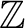 上の因数分解と言っても良い。)
これはそのまま素数
上の因数分解と言っても良い。)
これはそのまま素数 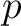 に依存して定義される剰余環
に依存して定義される剰余環
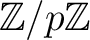 での因数分解とも考えられる。整数
での因数分解とも考えられる。整数 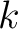 の
の
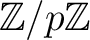 でのクラスを
でのクラスを
![$[k]_p$](img10.png) と書くと、
と書くと、
![$\displaystyle [1]_pX^5+[2]_p X^4+[7]_p X^3+[3]_p X^2 + [2]_p X-[15]_p =
([1]_p X^3+[4]_p X -[5]_p)([1]_pX^2+[2]_p X +[3]_p)
$](img11.png)
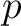 は素数でなくても整数であれば構わない。しかし
は素数でなくても整数であれば構わない。しかし 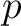 が素数ならば
が素数ならば
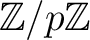 が体であるという利点があるので以下では主に
が体であるという利点があるので以下では主に 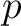 が素数の場合を
かんがえよう。
が素数の場合を
かんがえよう。
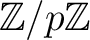 は体なので
は体なので
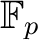 とも書くのであった。)
とも書くのであった。)
この分解についてもう少し考えてみる。
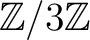 では
では
![$\displaystyle [1]_3X^5+[2]_3 X^4+[7]_3 X^3+[3]_3 X^2 + [2]_3 X-[15]_3 =
([1]_3 X^3+[4]_3 X -[5]_3)([1]_3X^2+[2]_3 X +[3]_3).
$](img14.png)
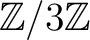 の元は
の元は
![$[0]_3,[1]_3,-[1]_3$](img15.png) のどれかに等しいから書き換えると:
のどれかに等しいから書き換えると:
![$\displaystyle [1]_3X^5-[1]_3 X^4+[1]_3 X^3- [1]_3 X =
([1]_3 X^3+[1]_3 X +[1]_3)([1]_3X^2-[1]_3 X )
$](img16.png)
![$[1]_3$](img17.png) のことは
のことは 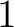 と書いてしまえば、
と書いてしまえば、
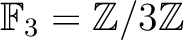 上で考えているという注釈
(
上で考えているという注釈
(
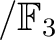 と略記することで以下では表現する)
のもとで
と略記することで以下では表現する)
のもとで
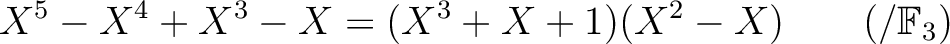
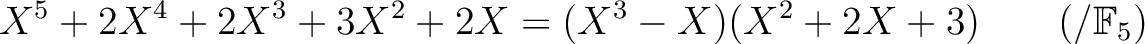 |
||
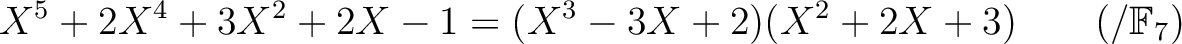 |
||
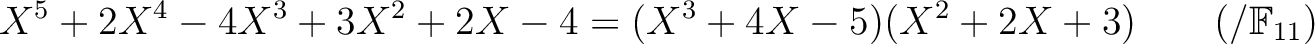 |
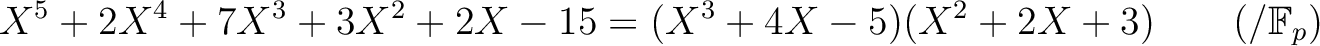
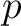 についていっぺんに書くことができるわけだが。
についていっぺんに書くことができるわけだが。
命題1.1 の対偶をとると次の命題を得る。
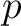 について
について
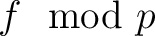 が
が
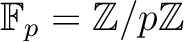 上既約ならば、
上既約ならば、
![$f(X)\in {\mbox{${\mathbb{Z}}$}}[X]$](img1.png) は
は
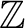 上で既約である。
上で既約である。