Next: About this document ...
巡回拡大
まずは今までの復習 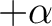 から。
から。
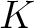 の有限次ガロア拡大
の有限次ガロア拡大 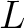 が与えられたとする。
が与えられたとする。
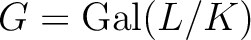 とおく。
このとき、
とおく。
このとき、
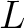 と
と 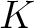 の間の中間体
の間の中間体 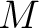 と、
と、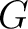 の部分群
の部分群 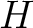 とが一対一に対応する。
とが一対一に対応する。
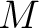 は
は 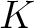 のガロア拡大である
のガロア拡大である
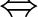
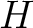 は
は 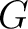 の正規部分群。
の正規部分群。
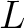 は体
は体 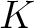 の有限次代数拡大体であるとする。
の有限次代数拡大体であるとする。
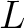 が
が 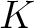 のアーベル拡大であるとは、
のアーベル拡大であるとは、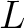 が
が 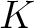 の
ガロア拡大であって、
の
ガロア拡大であって、
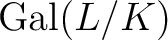 がアーベル群(=可換群)のときに言う。
がアーベル群(=可換群)のときに言う。
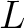 が
が 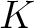 の巡回拡大であるとは、
の巡回拡大であるとは、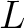 が
が 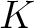 の
ガロア拡大であって、
の
ガロア拡大であって、
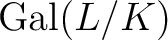 が巡回群のときに言う。
が巡回群のときに言う。
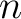 は正の整数であるとする。
は正の整数であるとする。
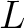 は体
は体 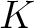 の有限次代数拡大体で、
の有限次代数拡大体で、![$[L:K]=n$](img11.png) とする。さらに、
とする。さらに、
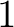 の
の 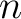 乗根が
乗根が
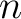 個
個 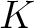 の中に含まれているとする。このとき、
の中に含まれているとする。このとき、
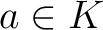 で、
で、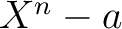 が
が 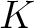 上既約であったとする。
このとき
上既約であったとする。
このとき 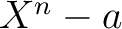 の根の一つ
の根の一つ 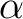 をとって、
をとって、
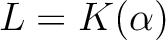 とおけば、
とおけば、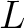 は
は
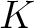 の
の 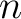 次巡回拡大である。
次巡回拡大である。
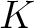 の
の 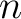 次巡回拡大体は上のようなものに限る。
次巡回拡大体は上のようなものに限る。